| [zurück] | 3.7. Abgeschrägtes Hexaeder |
[vor] |
 |
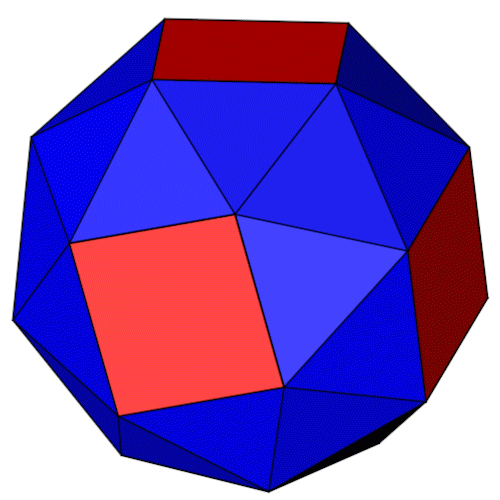 |
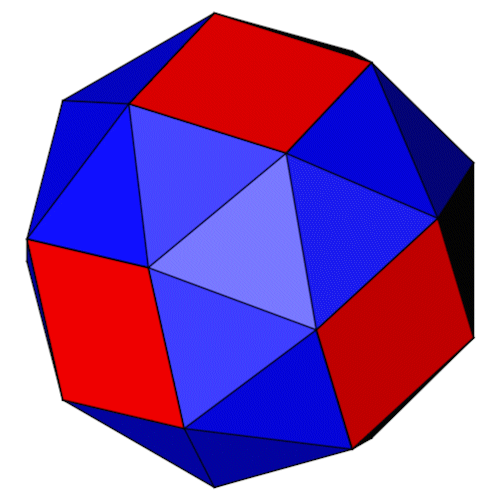
| Isometrie | Dimetrie |
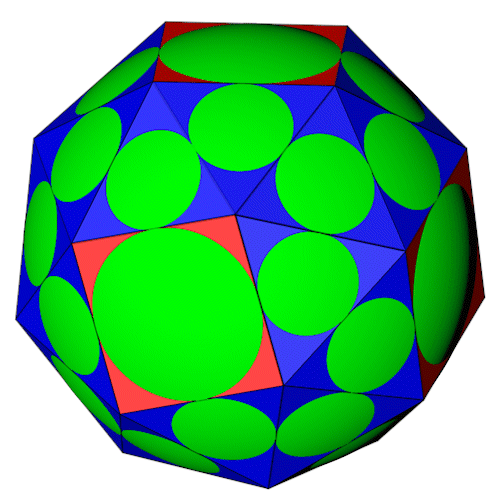
| Name | Abgeschrägtes Hexaeder Cubus simus Snub cube |
| Anzahl Ecken | 24 |
| Anzahl Kanten | 60 |
| Anzahl Flächen | 32 Dreiecke 6 Vierecke |
| Kantenlänge | a |
| Umkugelradius | 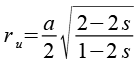 |
| Kantenkugelradius | 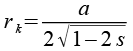 |
Mit

t ist die Tribonacci-Konstante.
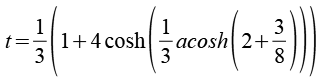 oder
oder

Für t gilt auch
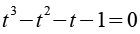
Eine etwas andere Schreibweise:
| Kantenlänge | 1 |
| Umkugelradius |  |
| Kantenkugelradius | 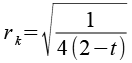 |
| Inkugelradius (Dreiecke) | 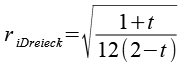 |
| Inkugelradius (Vierecke) | 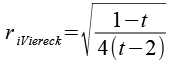 |
ru ist eine Lösung der Gleichung
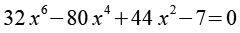
rk ist eine Lösung der Gleichung

riDreiecke ist eine Lösung der Gleichung
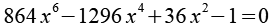
riVierecke ist eine Lösung der Gleichung

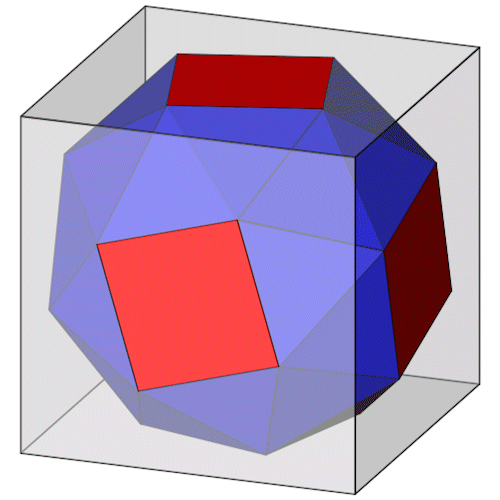
Das Abgeschrägte Hexaeder leitet sich vom Hexaeder ab. Die Quadrate des Abgeschrägten Hexaeders liegen auf den Seitenflächen des Hexaeders.
 |
 |
| Isometrie | Dimetrie |
Die drei Seitenansichten.



Das Abgeschrägte Hexaeder mit seiner Umkugel.

Das Große Abgeschrägte Hexaeder mit seiner Kantenkugel.
Die Koordinaten der Eckpunkte des Tetraederstumpfs lassen sich aus folgender Beziehung herleiten.
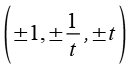
Durch Variation der Vorzeichen ergeben sich 8 Punkte, zur einfacheren Schreibweise führen wir d und e ein.
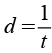
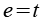
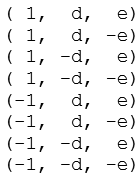
Daraus ergeben sich 48 Permutationen.
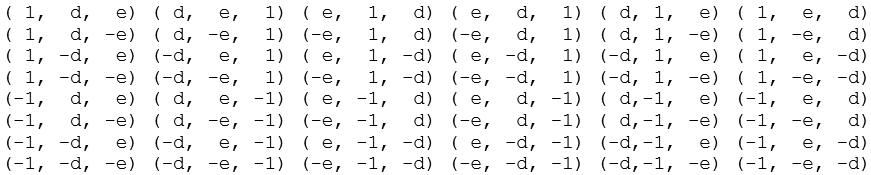
Dabei unterscheidet man zwischen gerader und ungerader Permutation. Für das Abgeschrägte Hexaeder wählen wir aus den ersten drei Spalten die Punkte mit ungerader Anzahl Plus Zeichen und aus den letzten drei Spalten die Punkte mit gerader Anzahl Plus Zeichen aus (rot).
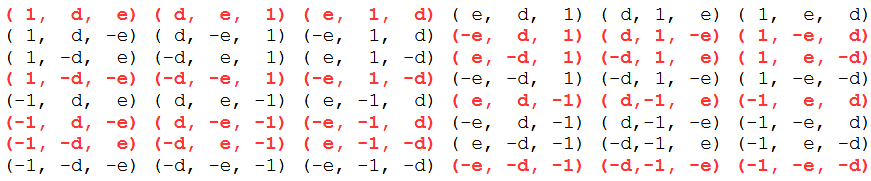
Die restlichen Punkte bilden einen zweiten chiralen Abgeschrägten Hexaeder.
Für die Kantenlänge a gilt.
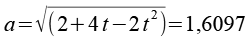
a ist eine Lösung der Gleichung.
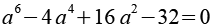
Die beiden chiralen Formen.
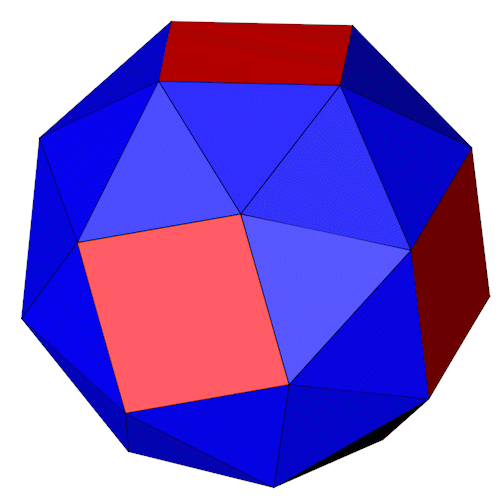 |
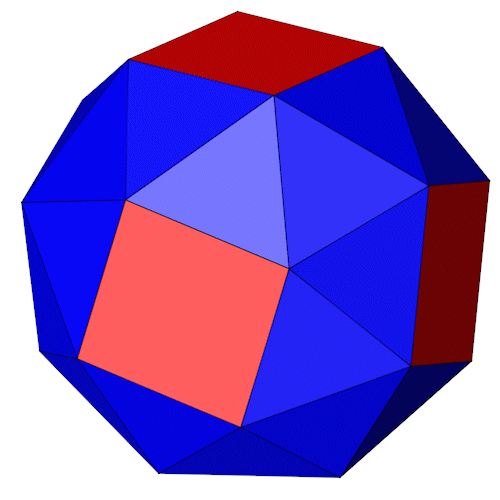 |
Beide Formen zusammen.

| [zurück] | [Inhaltsverzeichnis] | [vor] |