| [zurück] | 10.1. 8 Oktaeder |
[vor] |
8 Oktaeder lassen sich zu einem Ring verbinden.
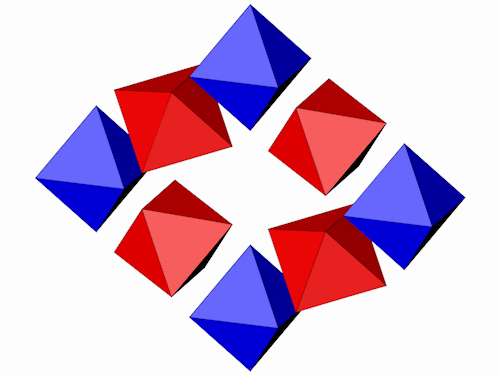

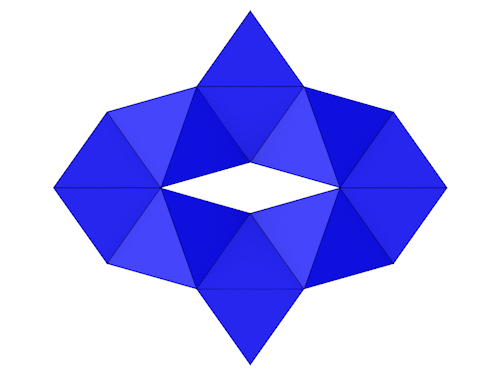

| Anzahl Ecken | 24 |
| Anzahl Flächen | 48 Dreiecke |
Die Lage der 8 Oktaeder zu berechnen erwies sich einfacher als gedacht. Die roten und grünen Eckpunkte liegen jeweils in einer Ebene.
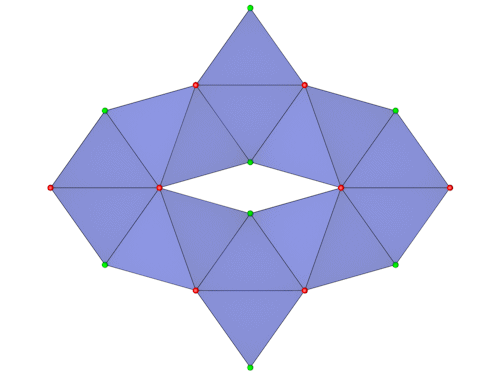
Aufgrund der Symmetrie ist es nur erforderlich zwei Punkte zu berechnen, der Rest läßt sich daraus ableiten.
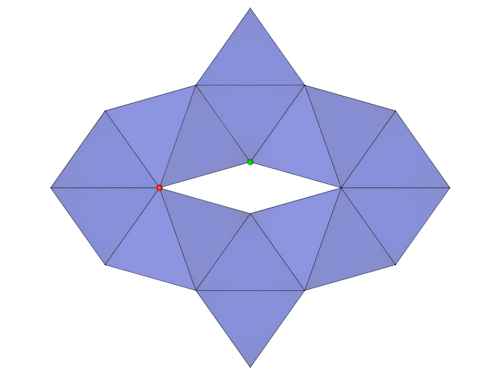
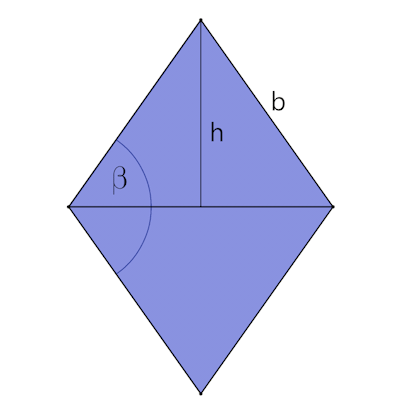
Höhen und Winkel im Oktaeder (Kantenlänge a) entnehmen wir einer Formelsammlung, die Seite b läßt sich über den Pythagoras berechnen.
![]()
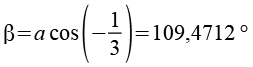
![]()
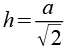
![]()
Um die beiden Punkte (rot und grün) zu berechnen benutzen wir das Dreieck mit den Seiten b, c und d.
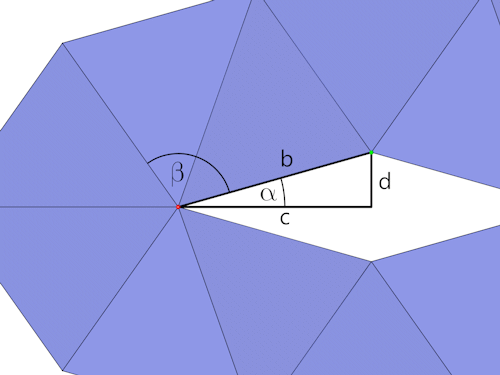
Der Winkel alpha läßt sich leicht aus dem Winkel beta ableiten.
![]()

Oder anders ausgedrückt.
![]()
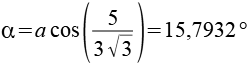
![]()
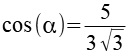
Über den Cosinus läßt sich die Seite c berechnen.
![]()
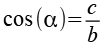
![]()
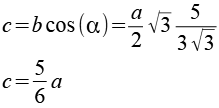
Aus b und c läßt sich die Seite d berechnen.
![]()
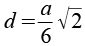
| [zurück] | [Inhaltsverzeichnis] | [vor] |