| [zurück] | 10.4. 10 Fünfecke in zwei Ebenen |
[vor] |
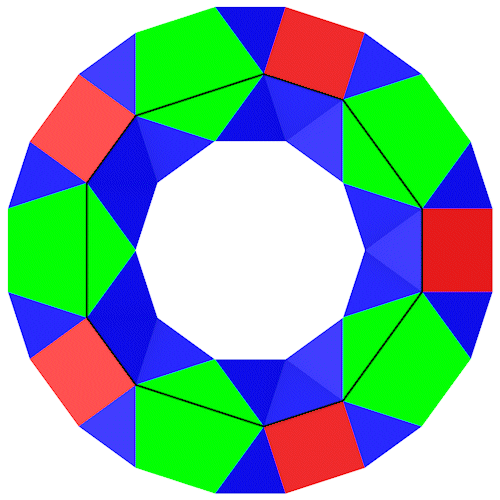
Aus 10 Fünfecken, die in zwei Ebenen im Kreis angeordnet sind, läßt sich ein interessanter Ring bilden.
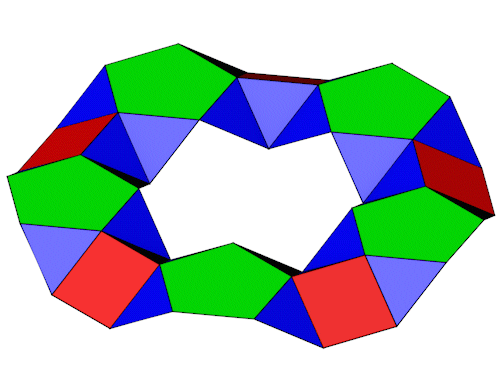 |
 |
| Anzahl Ecken | 50 |
| Anzahl Flächen | 50 Dreiecke 10 Vierecke 10 Fünfecke |
 |
 |
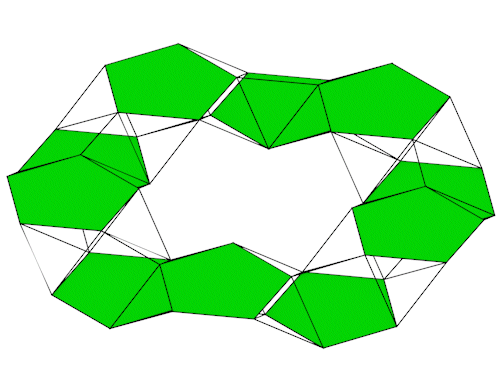 |
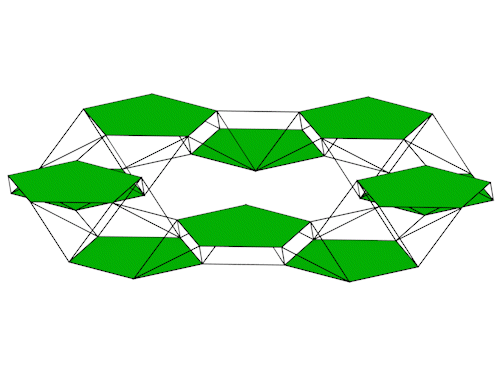 |
Die Seitenansichten.
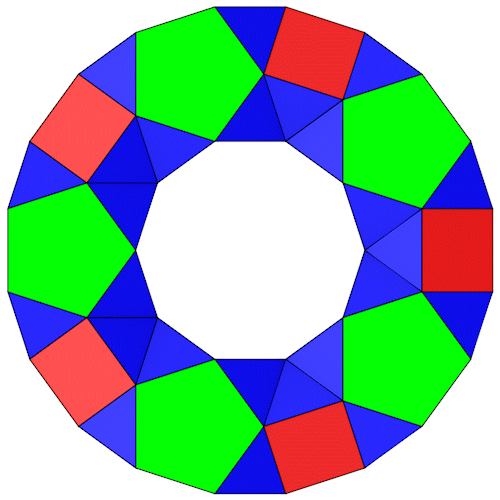


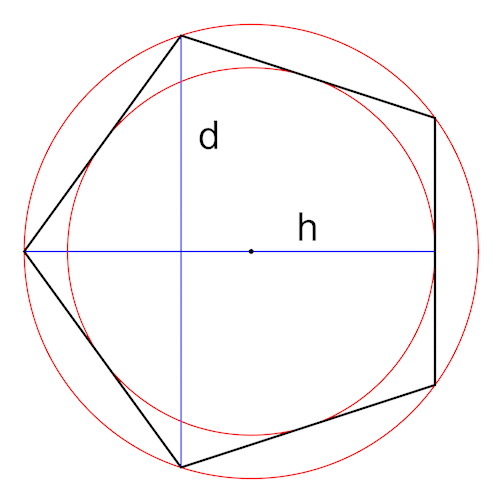
Für die Berechnung betrachten wir zuerst das Fünfeck (Kantenlänge = 1). Wichtig sind die Diagonale d, die Höhe h, der Inkreisradius ri und der Umkreisradius ru.


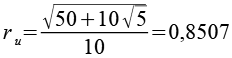
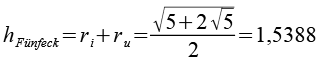
Die Diagonalen der Fünfecke und die Seiten der Vierecke bilden einen Ring.
Für die Berechnung betrachten wir die beiden gleichschenkligen Dreiecke.
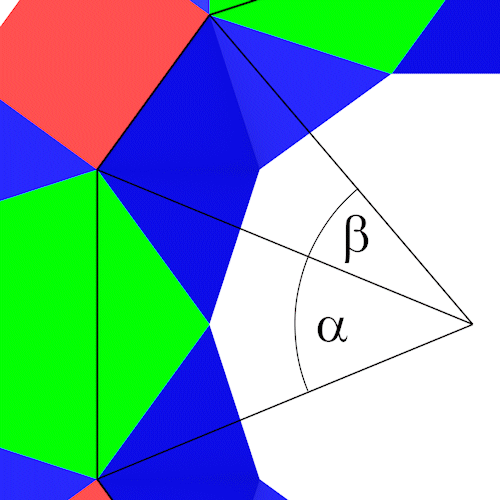
Für die Winkel gilt.
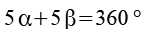
Für die beiden Winkel gilt.
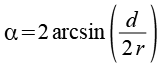
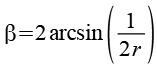
Die beiden Winkel setzen wir in obige Gleichung ein.
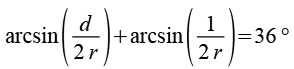
Um die Gleichung zu vereinfachen benutzen wir ein Additiostheorem aus einer Formelsammlung.
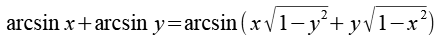
Damit erhalten wir.


Auf beiden Seiten wenden wir die Sinusfunktion an.
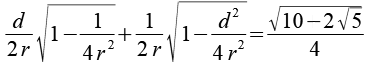
Leider müssen wir diese Gleichung numerisch lösen: r = 2,1243.
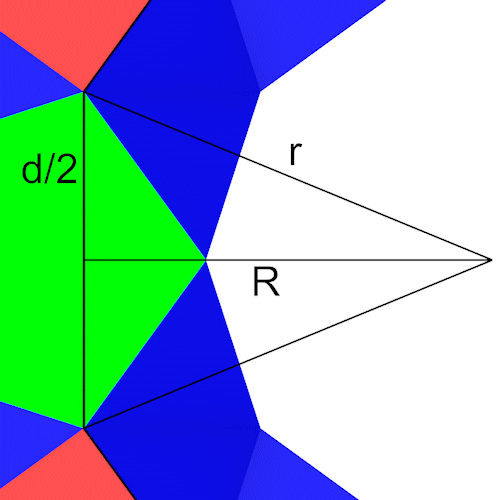
Den für den Polyederring nötigen Radius R berechnen wir mit dem Pythagoras.
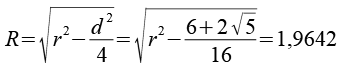
Jetzt müssen wir noch den Abstand der Funfeckebenen bzw. die Dicke des Polyederrings berechnen.
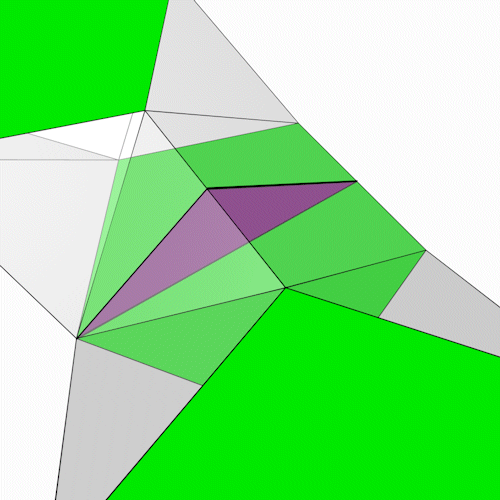
Auf dem grünen Fünfeck sitzt ein "Dach" aus einem Viereck und einem Dreieck, sie bilden das violette Dreieck. Die Höhe (hc) dieses Dreiecks ist der gesuchte Abstand. Die drei Seiten des Dreiecks sind a = 1, b = hDreieck und c = hFünfeck.
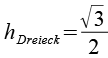
Für die Berechnung des Winkels beta benutzen wir den Cosinussatz aus einer Formelsammlung..
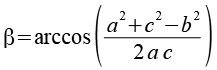
Für die gesuchte Höhe hc gilt.
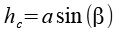
Für den Winkel beta erhalten wir.
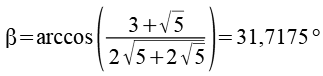
Für die gesuchte Höhe hc erhalten wir.
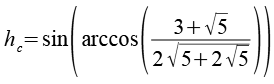
Mit Hilfe einer Formelsammlung läßt sich die Gleichung weiter vereinfachen.
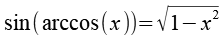
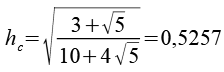
| [zurück] | [Inhaltsverzeichnis] | [vor] |