| [zurück] | 11.1. Rhombic Propello Octahedron |
[vor] |
Die Eckpunkte des Rhombic Propello Octahedron werden aus den ganzen Zahlen 1, 2, 3 und 4 gebildet [9].
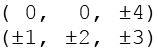
 |
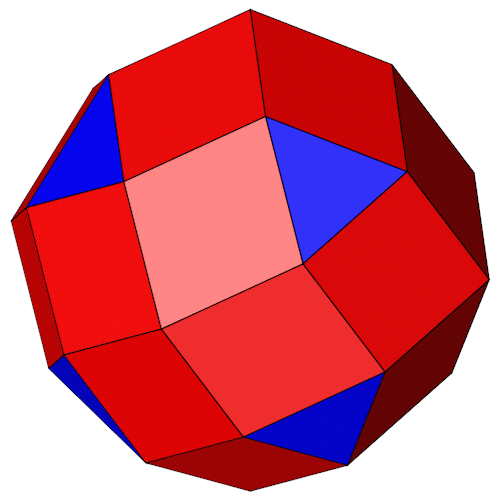 |
| Isometrie | Dimetrie |
| Name | Rhombic Propello Octahedron |
| Anzahl Ecken | 30 |
| Anzahl Flächen | 8 Dreiecke 24 Rauten |
Die Seitenansichten.



Die Koordinaten der Eckpunkte des Rhombic Propello Octahedrons lassen sich aus folgenden Beziehungen herleiten.
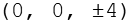
Daraus werden die 3 geraden Permutationen gebildet, andere gibt es in diesem Fall auch nicht.
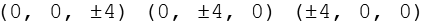
Durch Variation der Vorzeichen ergeben sich die ersten 6 Punkte.

Für die restlichen Punkte gilt.
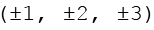
Daraus werden alle Permutationen gebildet, die 3 geraden Permutationen (links) und die 3 ungeraden Permutationen (rechts).
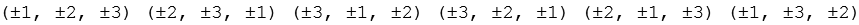
Durch Variation der Vorzeichen ergeben sich insgesamt 48 Punkte.
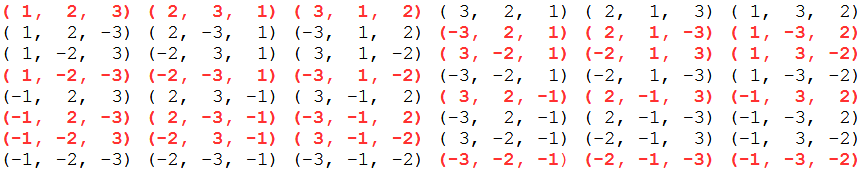
Aus den 48 Punkten werden 24 ausgewählt (rot). Von den geraden Permutationen alle mit gerader Anzahl Minuszeichen und von den ungeraden Permutationen alle mit ungerader Anzahl Minuszeichen. Die restlichen Punkte bilden einen zweiten chiralen Rhombic Propello Octahedron.
Die Kantenlänge a beträgt.
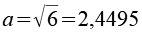
Die beiden chiralen Varianten.
 |
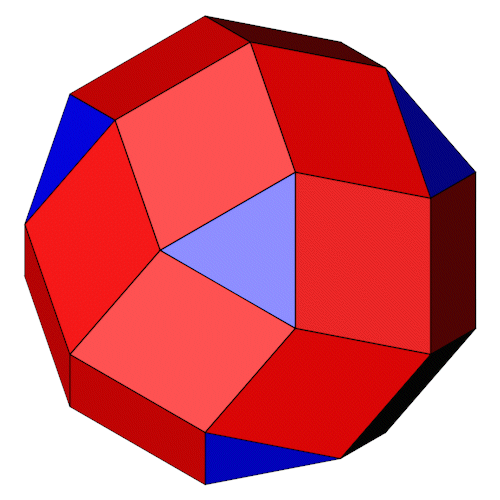 |
Beide chirale Varianten übereinander.

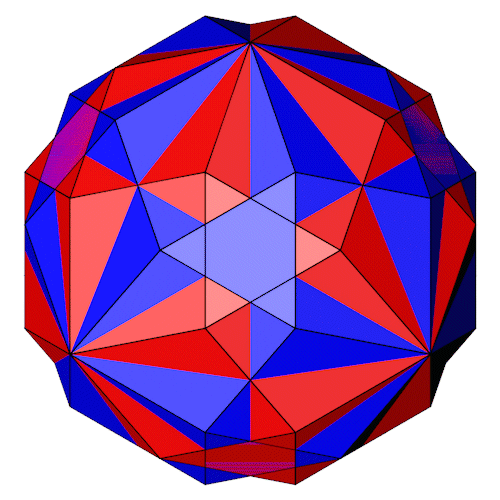
Beide Varianten unterschiedlich gefärbt.
In den Rhombic Propello Octahedron läßt sich ein Oktaeder einfügen.
 |
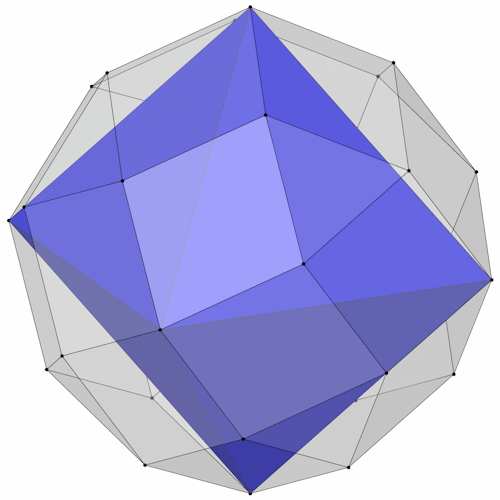 |
| Isometrie | Dimetrie |
Die Kantenlänge des Oktaeders beträgt.

Die Dreiecke des Rhombic Propello Octahedron liegen jeweils in Paaren parallel gegenüber, sie können daher zu Prismen verbunden werden.
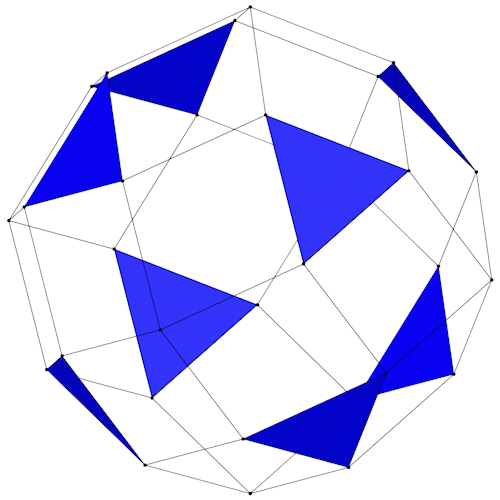
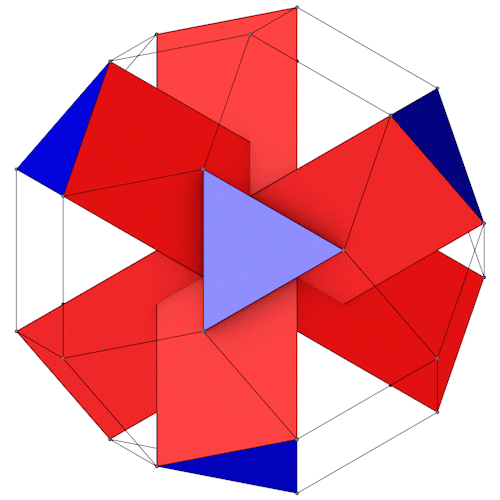 |
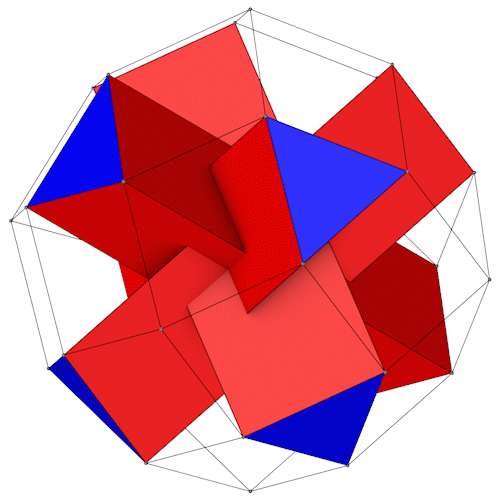 |
 |
 |
| Isometrie | Dimetrie |
Die Höhe der Prismen betragen.
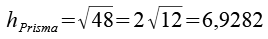
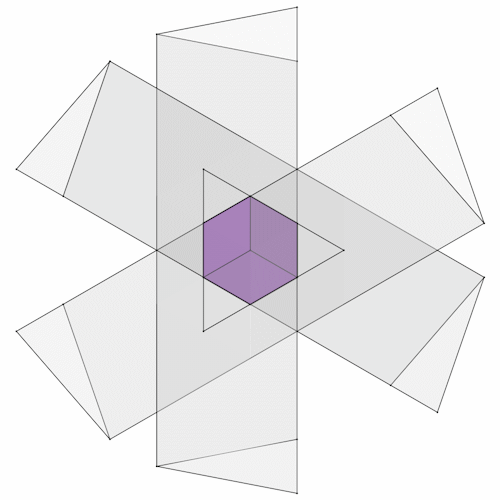
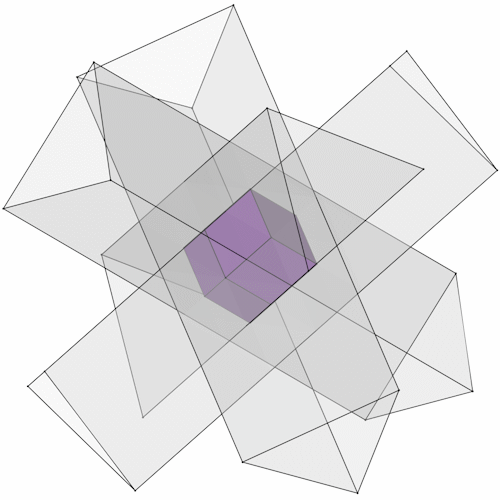
Die gemeinsame Schnittmenge der 4 Prismen ist ein Rhombendodekaeder (ein catalanischer Körper). Zur besseren Darstellung des Rhombendodekaeders habe ich nur ein Prisma dargestellt und es gekürzt.
Das Rhombendodekaeder hat die Kantenlänge a und den Inkugelradius ri.
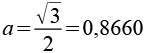
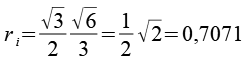
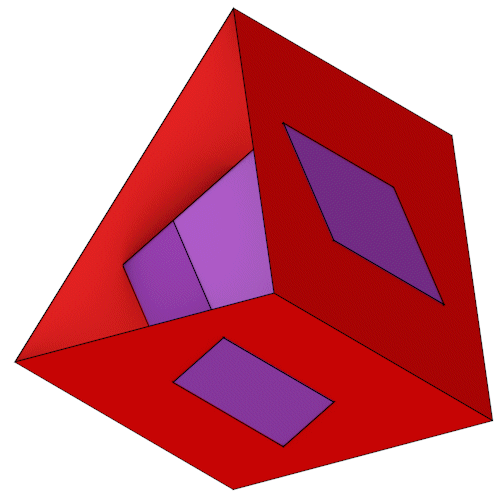
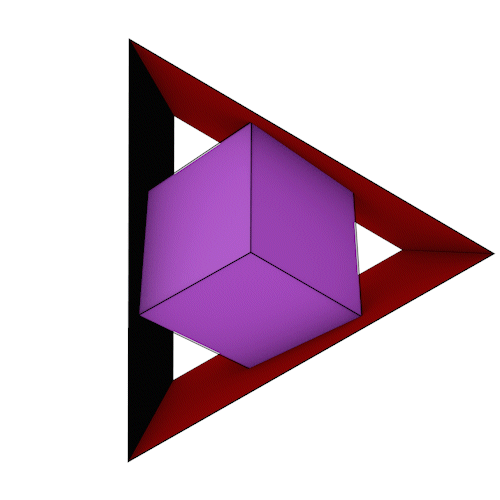
Jeweils eine Raute des Rhombendodekaeders liegt auf einer Seitenfläche eines Prismas. 2 Seiten der Raute liegen parallel zu den Seiten des Prismas. Schaut man in ein Prisma hinein bildet der Rhombendodekaeder ein Sechseck.
Der Inkugelradius des Rhombendodekaeder ist identisch mit dem Inkreiradius des Dreiecks (Rhombic Propello Octahedron). Dabei müssen die unterschiedlichen Kantenlängen berücksichtigt werden.
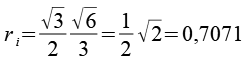 |
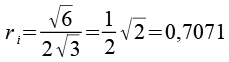 |
| Rhombendodekaeder | Dreieck (Rhombic Propello Octahedron) |
Wenn wir die Mittelpunkte der Dreiecke verbinden schneiden diese Geraden die Eckpunkte des Rhombendodekaeders.

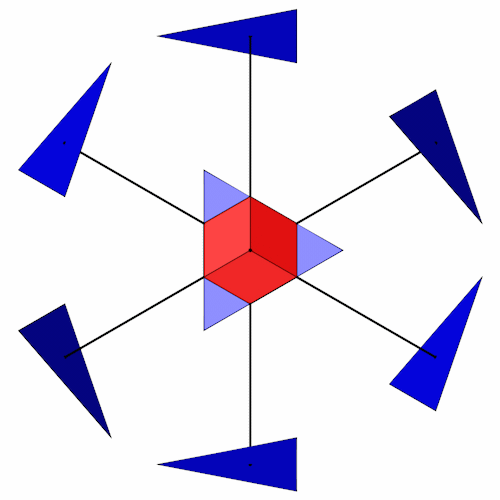
Die Mittelpunkte der Dreiecke sind wie folgt definiert.
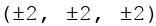
Durch Variation der Vorzeichen ergeben sich die 8 Punkte. Punkte, die die gleiche Anzahl Plus und Minuszeichen haben, liegen gegenüber (gleiche Farbe).
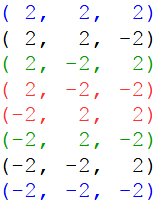
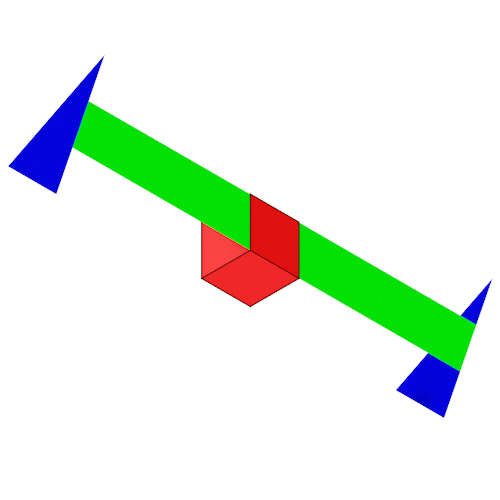
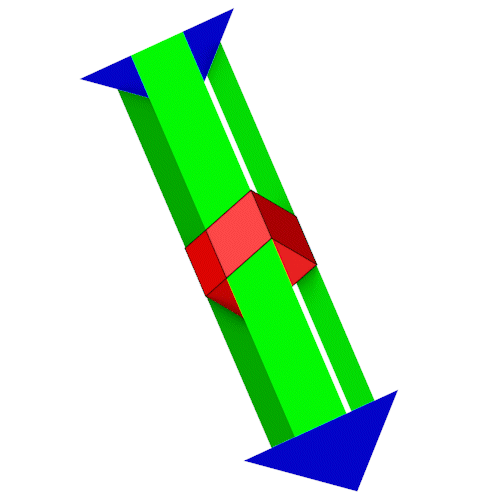
Betrachten wir eine Raute des Rhombendodekaeders etwas genauer.
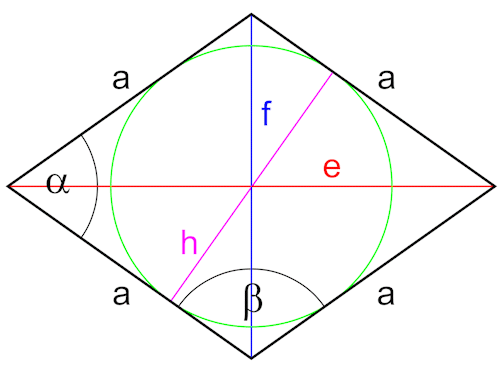
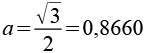


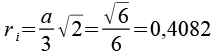
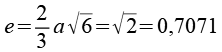
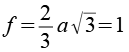
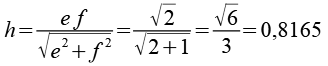
Die Höhe der Raute beträgt ein Drittel der Kantenlänge des Rhombic Propello Octahedrons. Verbinden wir so zwei Dreiecke mit dem Rhombendodekaeder.
| [zurück] | [Inhaltsverzeichnis] | [vor] |