| [zurück] | 3.2. Kuboktaeder |
[vor] |
 |
 |
| Isometrie | Dimetrie |
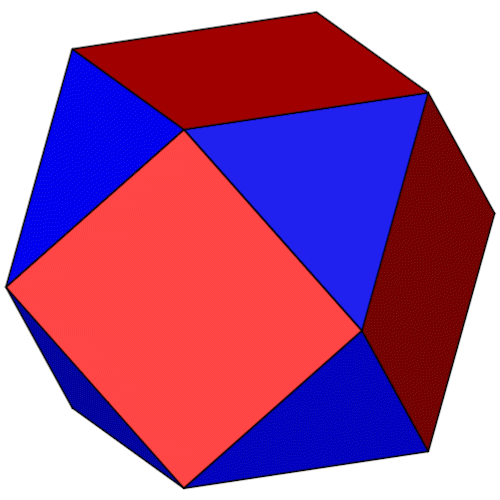
| Name | Kuboktaeder Cuboctahedron |
| Anzahl Ecken | 12 |
| Anzahl Kanten | 24 |
| Anzahl Flächen | 8 Dreiecke 6 Vierecke |
| Kantenlänge | a |
| Umkugelradius | 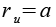 |
| Kantenkugelradius | 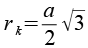 |
| Inkugelradius (Dreiecke) | 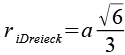 |
| Inkugelradius (Vierecke) |  |
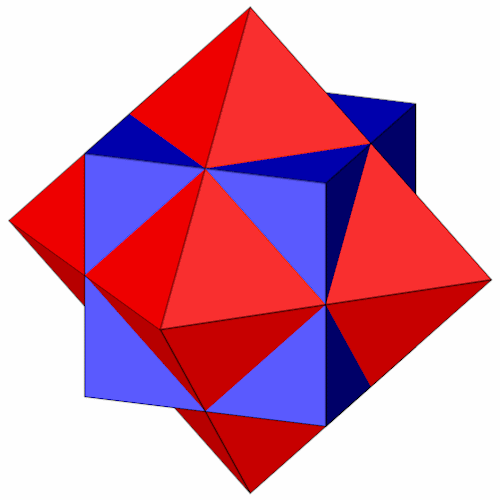
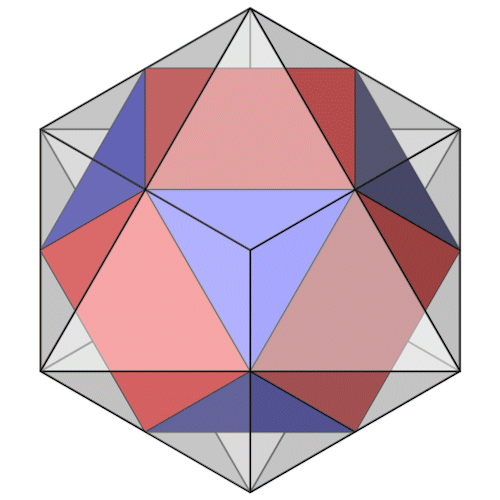
Der Kuboktaeder läßt sich auf verschiedenem Wege konstruieren. Aus der Schnittmenge eines Hexaeders und eines Oktaeders.
 |
 |
 |
 |
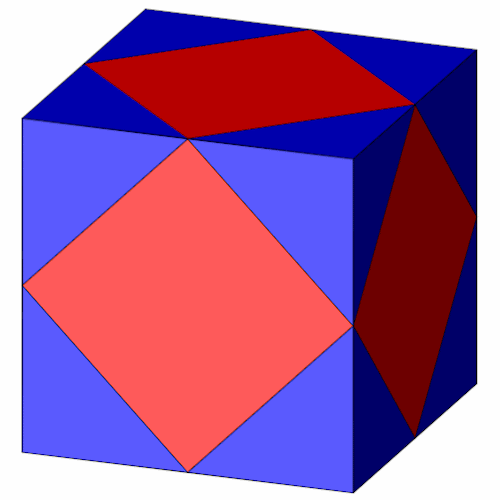
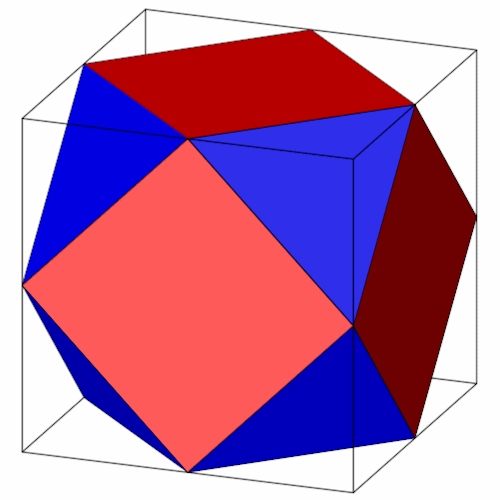
Durch Abstumpfen eines Hexaeders.
 |
 |
Durch Abstumpfen eines Oktaeders.
 |
 |
Die drei Seitenansichten.



Der Kuboktaeder mit seiner Umkugel.

Der Kuboktaeder mit seiner Kantenkugel.

Den Kuboktaeder kann man in zwei Dreieckskuppeln (Johnson Körper J3) zerschneiden.

Der Kuboktaeder (blau) mit seinem dualen Körper, dem Rhombendodekaeder (rot). Der duale Körper bildet auf den Flächen des Kuboktaeders gleichmäßige Pyramiden.

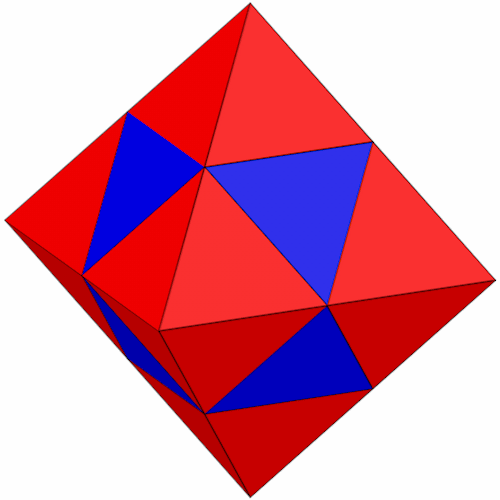
Die Koordinaten der Eckpunkte des Kuboktaeders lassen sich aus folgender Beziehung herleiten.
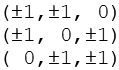
Durch Variation der Vorzeichen ergeben sich 12 Punkte, für die Kantenlänge a gilt.
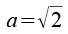
Vom Kuboktaeder bzw. seinen Koordinaten lassen sich weitere Polyeder ableiten.
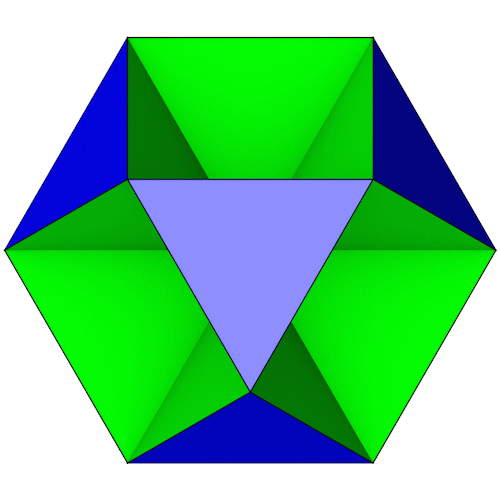
Oktahemioktaeder
 |
 |
 |
 |
| Anzahl Ecken | 12 |
| Anzahl Flächen | 8 Dreiecke 4 Sechsecke |
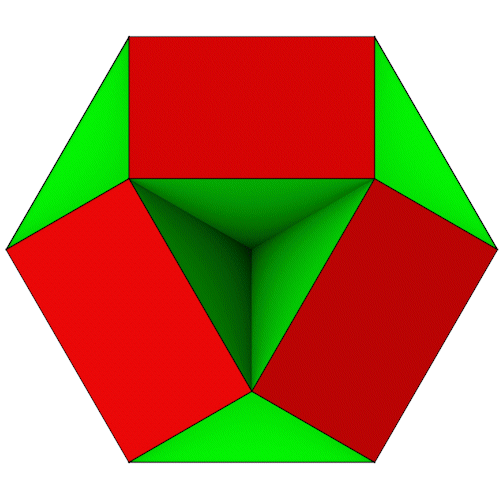
Kubohemioktaeder
 |
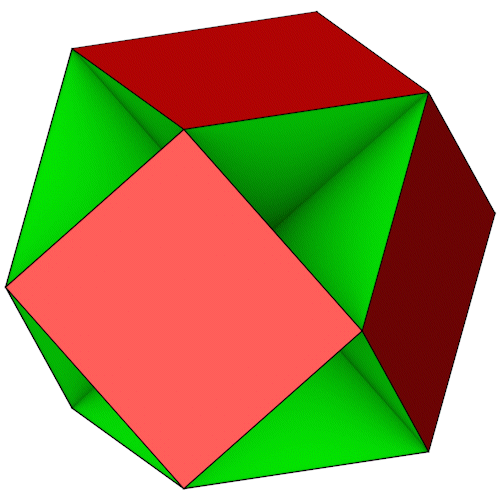 |
| Anzahl Ecken | 12 |
| Anzahl Flächen | 6 Vierecke 4 Sechsecke |
| [zurück] | [Inhaltsverzeichnis] | [vor] |