Interessante Mathe Aufgaben
|
[zurück] | Interessante Mathe Aufgaben |
[vor] | |
Wir haben 3 Gleichungen mit 3 Unbekannten.
(Gl. 1)
(Gl. 2)
(Gl. 3)
Gl. 1 wird quadriert.
(Gl. 4)
Es gilt:
(Gl. 5)
Mit Hilfe von Gl. 5 erhalten wir aus Gl. 4.
(Gl. 6)
Gl. 2 setzen wir in Gl. 6 ein.
(Gl. 7)
Auf beiden Seiten subtrahieren wir 98.
(Gl. 8)
Beide Seiten teilen wir durch 2.
(Gl. 9)
Im nächsten Schritt quadrieren wir Gl. 3.
(Gl. 10)
Mit Hilfe von Gl. 5 erhalten wir aus Gl. 10.
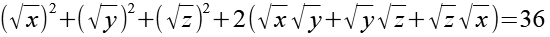(Gl. 11)
Es gilt:
(Gl. 12)
Wurzel und Quadrat heben sich auf, mit Hilfe von Gl. 12 erhalten wir aus Gl. 11.
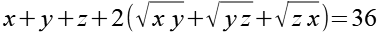(Gl. 13)
Gl. 1 setzen wir in Gl. 13 ein.
(Gl. 14)
Auf beiden Seiten subtrahieren wir 14.
(Gl. 15)
Beide Seiten teilen wir durch 2.
(Gl. 16)
Gl. 16 wird quadriert.
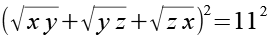(Gl. 17)
Mit Hilfe von Gl. 5 erhalten wir aus Gl. 17.
(Gl. 18)
Wurzel und Quadrat heben sich auf.
(Gl. 19)
Eine Wurzel können wir ausklammern.
(Gl. 20)
Gl. 9 und Gl. 3 setzen wir in Gl. 20 ein.
(Gl. 21)
Auf beiden Seiten subtrahieren wir 49.
(Gl. 22)
Beide Seiten teilen wir durch 12.
(Gl. 23)
Beide Seiten werden quadriert.
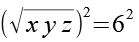(Gl. 24)
Wurzel und Quadrat heben sich auf.
(Gl. 25)
Mit Gl. 25, Gl. 1 und Gl. 9 erhalten wir wieder ein System aus 3 Gleichungen mit 3 Unbekannten.
)
Wir betrachten x, y und z als Lösung einer Kubischen Gleichung.
(Gl. 26)
Nach Ausmultiplizieren der Klammern erhalten wir.
(Gl. 27)
(Gl. 28)
(Gl. 29)
Gl. 25, Gl. 1 und Gl. 9 setzen wir in Gl. 29 ein.
(Gl. 30)
Aufgrund der Koeffizienten können wir die erste Lösung raten.
(Gl. 31)
Zur Kontrolle setzen wir Gl. 31 in Gl. 30 ein.
(Gl. 32)
Gl. 30 teilen wir durch Lösung 1.
(Gl. 33)
(Gl. 34)
Wir erhalten eine quadratische Gleichung.
(Gl. 35)
Für die Lösung einer quadratische Gleichung gilt:
(Gl. 36)
(Gl. 37)
Mit Hilfe von Gl. 37 erhalten wir die 2 Lösungen der quadratische Gleichung.
(Gl. 38)
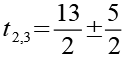(Gl. 39)
(Gl. 40)
(Gl. 41)
Für die Lösung von Gl. 1-3 erhalten wir 6 Permutationen.
(Gl. 42)
Zur Kontrolle setzen wir die Lösung x = 1, y = 4 und z = 9 in Gl.1-3 ein.
Das gilt natürlich auch für das zweite Gleichungssystem (Gl. 25, Gl. 1 und Gl. 9).
Anhang
Alternative Löung der quadratischen Gleichung 35 ohne p,q Formel (Gl. 37).
(Gl. 35)
Die -13 ersetzen wir durch -4-9.
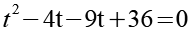(Gl. 43)
In Gl. 43 können wir einmal t und einmal -9 ausklammern.
(Gl. 44)
In Gl. 44 können wir (t - 4) ausklammern. So erhalten wir ebenfalls die Lösungen 4 und 9.
(Gl. 45)
Alternativer Lösungsansatz für die Gleichungen 1 bis 3. Betrachten wir Gl. 3.
(Gl. 3)
Die Summe der drei Wurzeln ist eine ganze Zahl, daraus folgt das auch die Wurzeln von x, y und z ganze Zahlen sein müssen. Das ist der Fall wenn x, y und z ebenfalls ganze Zahlen sind (0, 1, 4, 9, 16, 25, ...).
Setzen wir verschiedene Kombinationn in Gl. 3 ein.
(Gl. 46)
(Gl. 47)
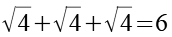(Gl. 48)
Gl. 46 widerspricht Gl.3 und kommt als Lösung nicht in Frage. Gl. 48 erfüllt zwar Gl. 3 aber x = y = z = 4 widerspricht Gl. 1. Die korrekte Lösung zeigt Gl. 47.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |