[zurück]

Interessante Mathe Aufgaben

 [vor]

Bei dieser Aufgabe geht es nicht darum eine Gleichung zu lösen sondern den Ausdruck ohne Benutzung eines Taschenrechners zu vereinfachen.

      (Gl. 1)

Die 3 ziehen wir vor das Summenzeichen.

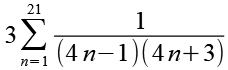      (Gl. 2)

Die Laufvariable multiplizieren wir mit 4, den Faktor vor dem Summenzeichen müssen wir entsprechend durch 4 teilen.

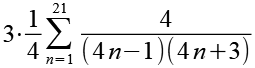      (Gl. 3)

Um die Laufvariable zu vereinfachen addieren wir zum Zähler 4n-4n, der Wert der LKaufvariable wir dadurch nicht verändert da 4n-4n gleich Null ist.

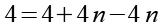      (Gl. 4)

Die 4 auf der rechten Seite ersetzen wir durch 3+1.

      (Gl. 5)

Die rechte Seite ordnen wir etwas anders an.

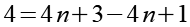      (Gl. 6)

      (Gl. 7)

Gl. 7 setzen wir in Gl. 3 ein.

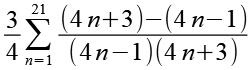      (Gl. 8)

Die Laufvariable können wir in eine Summe aus zwei Brüchen aufspalten.

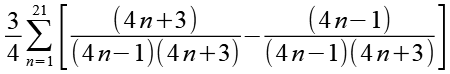      (Gl. 9)

In jedem Bruch läßt sich eine Klammer kürzen.

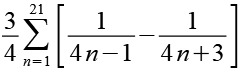      (Gl. 10)

Wir definieren eine Funktion f(n).

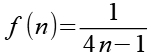      (Gl. 11)

Durch Einsetzen von n+1 erzeugen wir daraus die Funktion f(n+1).

      (Gl. 12)

Gl. 11 und Gl. 12 setzen wir in Gl. 10 ein.

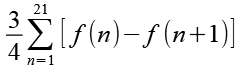      (Gl. 13)

Wir führen die Summenfunktion aus (n=1 bis n=21).

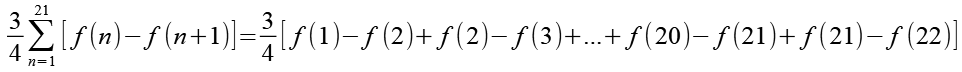      (Gl. 14)

Bis auf f(1) und f(22) heben sich benachbarte Glieder auf, z.B. -f(2)+f(2). Wir erhalten als Resultat.

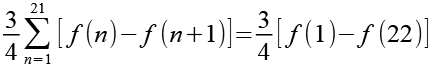      (Gl. 15)

Für f(1) und f(22) erhalten wir.

      (Gl. 16)

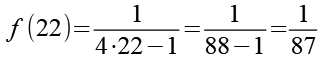      (Gl. 17)

Gl. 16 und Gl. 17 setzen wir in Gl. 15 ein.

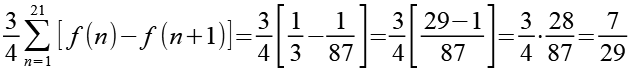      (Gl. 18)

Das Ergebnis.

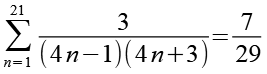      (Gl. 19)

Anhang 1

Untersuchen wir die Konvergenz der Reihe.

n
1   
2   
3   
4   
5   
6   
7   
8   
9   
10   
11   
12   
13   
14   
15   
16   
17   
18   
19   
20   
21   		     0,142857142857
    0,181818181818
    0,200000000000
    0,210526315789
    0,217391304348
    0,222222222222
    0,225806451613
    0,228571428571
    0,230769230769
    0,232558139535
    0,234042553191
    0,235294117647
    0,236363636364
    0,237288135593
    0,238095238095
    0,238805970149
    0,239436619718
    0,240000000000
    0,240506329114
    0,240963855422
    0,241379310345

Anhang 2

Bei 21 Reihengliedern kann man das Ergebnis auch direkt berechnen.

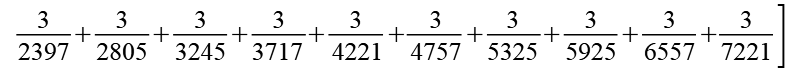      (Gl. 20)

Die Brüche wurden nummeriert (a1 bis a21).

      (Gl. 21)

Die Brüche werden zuerst paarweise addiert. Um das Kürzen zu vereinfachen habe ich bei den Nennern die Primfaktorzerlegung eingesetzt.

      (Gl. 22)

      (Gl. 23)

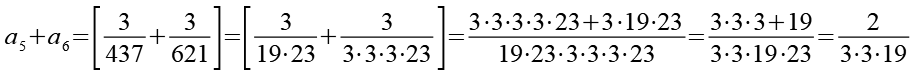      (Gl. 24)

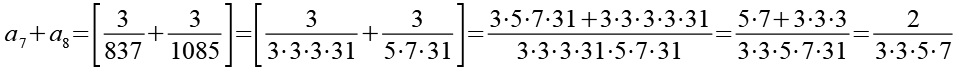      (Gl. 25)

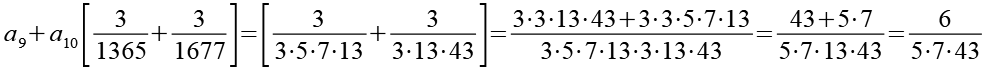      (Gl. 26)

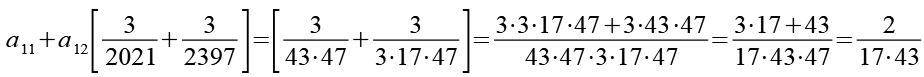      (Gl. 27)

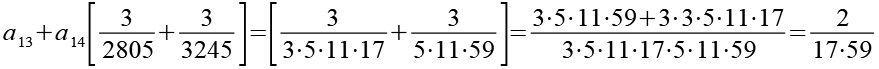      (Gl. 28)

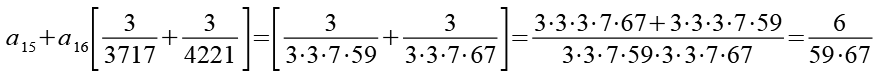      (Gl. 29)

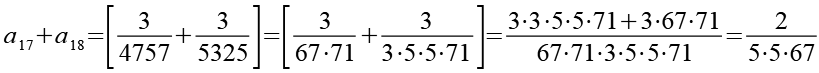      (Gl. 30)

      (Gl. 31)

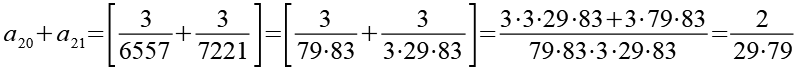      (Gl. 32)

Im zweiten Schritt werden die ersten 11 Teilsummen addiert.

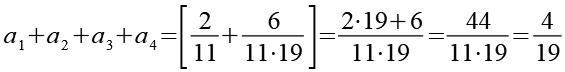      (Gl. 33)

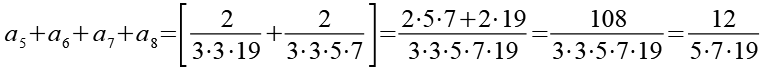      (Gl. 34)

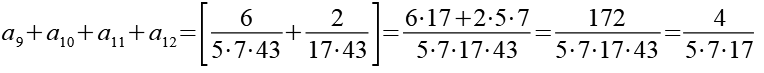      (Gl. 35)

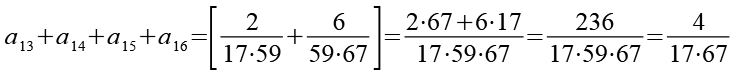      (Gl. 36)

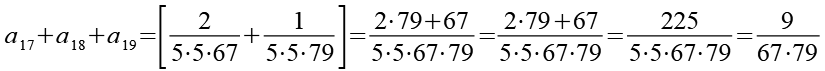      (Gl. 37)

      (Gl. 38)

Im dritten Schritt werden die zweiten 6 Teilsummen addiert.

      (Gl. 39)

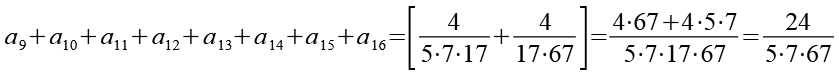      (Gl. 40)

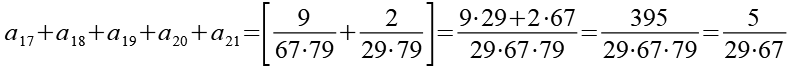      (Gl. 41)

Im vierten Schritt werden die dritten 3 Teilsummen addiert.

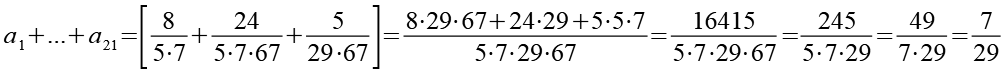      (Gl. 42)

[zurück] [Inhaltsverzeichnis] [vor]