[zurück]

Aufgabe 37

[vor]

Bei dieser Aufgabe geht es nicht darum eine Gleichung zu lösen sondern den Ausdruck ohne Benutzung eines Taschenrechners zu vereinfachen.

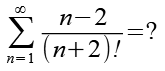      (Gl. 1)

Wir ersetzen die -2 in Gl. 1 durch +2-4.

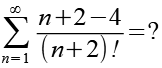      (Gl. 2)

Dadurch können wir den Bruch in zwei Teilbrüche trennen.

      (Gl. 3)

Es gilt für die Fakultät.

      (Gl. 4)

(n + 2)! im ersten Bruch ersetzen wir durch Gl. 4.

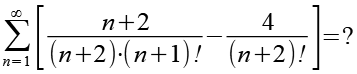      (Gl. 5)

(n + 2) können wir kürzen.

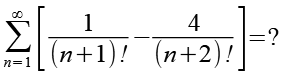      (Gl. 6)

Gl. 6 trennen wir in zwei Summenfunktionen.

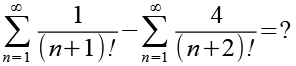      (Gl. 7)

Den Faktor 4 ziehen wir vor die Summe.

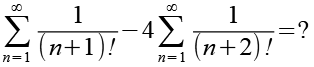      (Gl. 8)

Für die Potenzreihe der Exponentialfunktion gilt.

      (Gl. 9)

Wir setzen x=1 ein und erhalten aus Gl. 9.

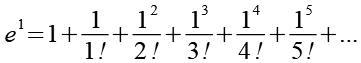      (Gl. 10)

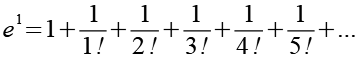      (Gl. 11)

Die erste Summe aus Gl. 8 führt zu folgender Reihenentwicklung.

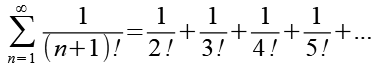      (Gl. 12)

Diese Reihenentwicklung können wir auch durch Gl. 11 darstellen.

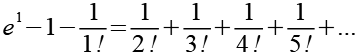      (Gl. 13)

Gl. 13 setzen wir in Gl. 12 ein.

      (Gl. 14)

Mit der 2. Summe aus Gl. 8 verfahren wir genauso.

      (Gl. 15)

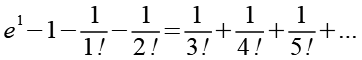      (Gl. 16)

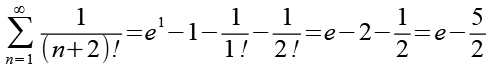      (Gl. 17)

Gl. 14 und Gl. 17 setzen wir in Gl. 8 ein.

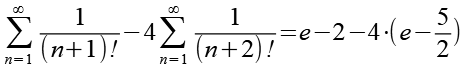      (Gl. 18)

      (Gl. 19)

Das Ergebnis.

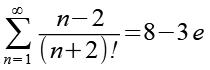      (Gl. 20)

Anhang

Untersuchen wir die Konvergenz der Reihe.

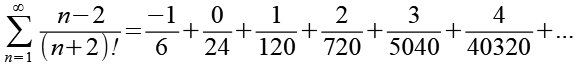      (Gl. 21)

      (Gl. 22)

[zurück]

[Inhaltsverzeichnis]

[vor]