Aufgabe 39
|
[zurück] | Aufgabe 39 |
[vor] | |
Bei dieser Aufgabe geht es nicht darum eine Gleichung zu lösen sondern den Ausdruck ohne Benutzung eines Taschenrechners zu vereinfachen.
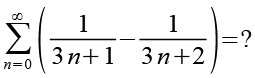(Gl. 1)
Der Lösungsweg ist etwas ungewöhnlich, betrachten wir zuerst die Potenzfunktion xn.
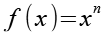(Gl. 2)
Wenn wir Gl. 2 integrieren erhalten wir.
(Gl. 3)
Die Integration wiederholen wir mit der Potenzfunktion x3n. Der Nenner (3n+1) entspricht schon der Gl. 1, jetzt müssen wir nur noch den Zähler loswerden.
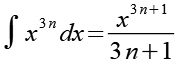(Gl. 4)
Dazu integrieren wir Gl. 4, als Integrationsgrenzen wählen wir 0 und 1.
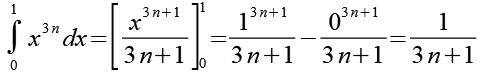(Gl. 5)
Damit haben wir den ersten Bruch in Gl. 1 durch ein Integral ersetzt.
(Gl. 6)
(Gl. 7)
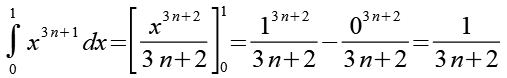(Gl. 8)
Damit haben wir auch den zweiten Bruch in Gl. 1 durch ein Integral ersetzt.
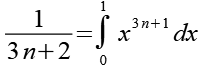(Gl. 9)
Jetzt setzen wir Gl. 6 und Gl. 9 in Gl. 1 ein.
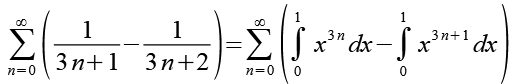(Gl. 10)
Die beiden Integrale fügen wir zu einem Integral zusammen.
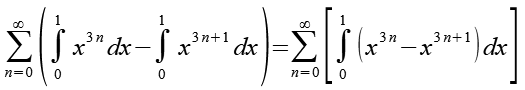(Gl. 11)
Wir tauschen die Position der Summenfunktion und des Integrals.
(Gl. 12)
Jetzt können wir (1-x) ausklammern.
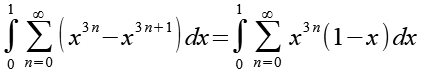(Gl. 13)
Da (1-x) nicht von n abhängt können wir (1-x) vor die Summenfunktion ziehen.
(Gl. 14)
Für die Reihenentwicklung der geomnetrischen Reihe gilt (|x|<1).
(Gl. 15)
Es gilt.
(Gl. 16)
Mit Hilfe von Gl. 15 und Gl. 16 erhalten wir für die Potenzfunktion x3n.
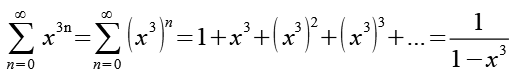(Gl. 17)
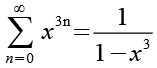(Gl. 18)
Gl. 18 setzen wir in Gl. 14 ein.
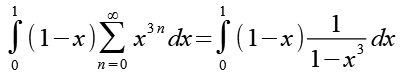(Gl. 19)
Es gilt.
(Gl. 20)
Mit Hilfe von Gl. 20 erhalten wir.
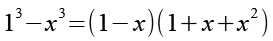(Gl. 21)
Gl. 21 setzen wir in Gl. 19 ein.
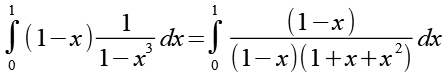(Gl. 22)
Jetzt können wir (1-x) kürzen.
(Gl. 23)
Den Nenner formen wir so um das er der Summen zweier Quadrate entspricht.
(Gl. 24)
Gl. 24 setzen wir in Gl. 23 ein.
(Gl. 25)
Für das Integral dieser Funktion gilt allgemein.
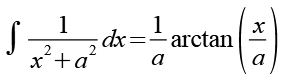(Gl. 26)
Gl. 26 wenden wir auf Gl. 25 an.
(Gl. 27)
(Gl. 28)
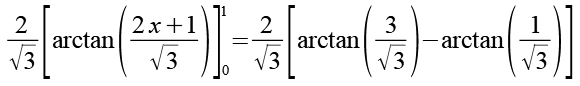(Gl. 29)
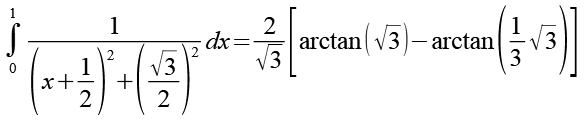(Gl. 30)
Für die beiden arctan Funktionen gilt (siehe auch Angang 2).
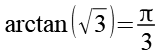(Gl. 31)
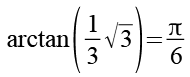(Gl. 32)
Gl. 31 und Gl. 32 setzen wir in Gl. 30 ein.
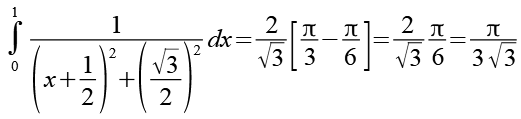(Gl. 33)
Damit haben wir auch die Lösung von Gl. 1.
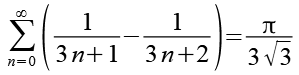(Gl. 34)
Die einzelnen Schritte dieser Berechnung habe ich noch einmal zusammengefasst.
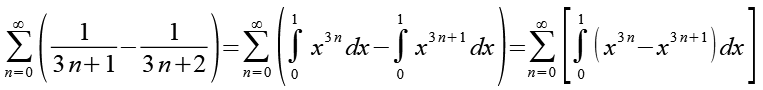(Gl. 35)
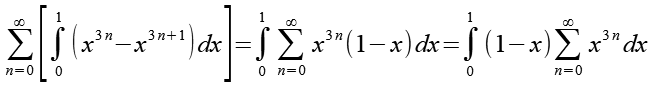(Gl. 36)
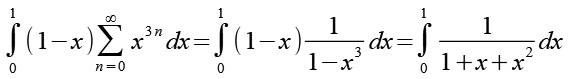(Gl. 37)
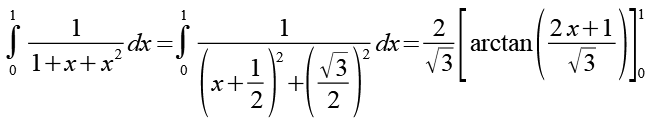(Gl. 38)
(Gl. 39)
Anhang 1
Untersuchen wir die Konvergenz der Reihe.
| n | |
|
1 10 100 1000 10000 100000 1000000 10000000 100000000 |
0,550000000000 0,594504944711 0,603499686055 0,604488787975 0,604588678078 0,604598676978 0,604599676967 0,604599776965 0,604599785954 0,604599788078 |
Anhang 2
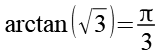(Gl. 31)
Überprüfen wir den arctan durch sin und cos.
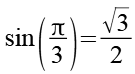(Gl. 40)
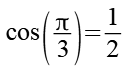(Gl. 41)
Es gilt.
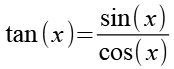(Gl. 42)
Gl. 40 und Gl. 41 setzen wir in Gl. 42 ein.
(Gl. 43)
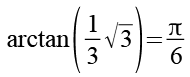(Gl. 32)
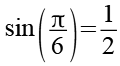(Gl. 44)
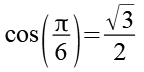(Gl. 45)
Gl. 4 und Gl. 45 setzen wir in Gl. 42 ein.
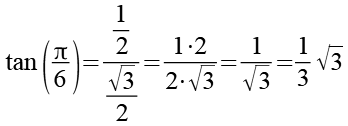(Gl. 46)
Anhang 3
Mit einer guten Formelsammlung kann man sich die Umformung nach Gl. 24 sparen. Für das Integral gilt (für b2 - 4 a c < 0).
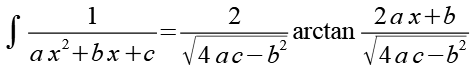(Gl. 47)
Für unser Beispiel gilt.
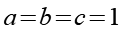(Gl. 48)
(Gl. 49)
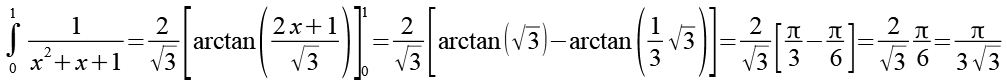(Gl. 50)
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |