[zurück]

Aufgabe 45

 [vor]

Ziel der Aufgabe ist es alle 6 Lösungen für x zu finden.

      (Gl. 1)

Auf der linken Seite klammern wir im Zähler und Nenner einmal x aus.

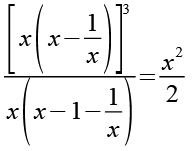      (Gl. 2)

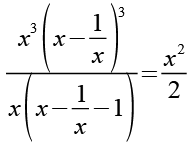      (Gl. 3)

Auf der linken Seite können wir einmal x kürzen.

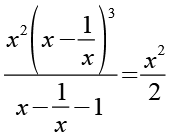      (Gl. 4)

Beide Seiten dividieren wir durch x2.

      (Gl. 5)

Auf beiden Seiten bilden wir den Kehrwert.

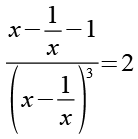      (Gl. 6)

Den Bruch teilen wir in zwei Brüche.

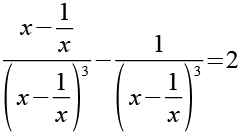      (Gl. 7)

Im linken Bruch können wir x-(1/x) kürzen.

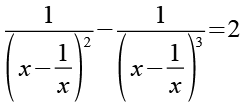      (Gl. 8)

Wir ersetzen 1 durch 12 bzw. 13.

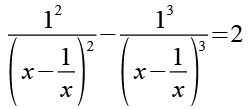      (Gl. 9)

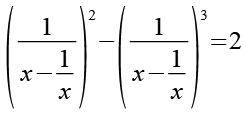      (Gl. 10)

Wir substituieren den Inhalt der Klammer durch t.

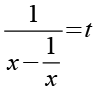      (Gl. 11)

Wir setzen Gl. 11 in Gl. 10 ein.

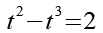      (Gl. 12)

Auf beiden Seiten subtrahieren wir 2.

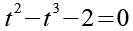      (Gl. 13)

Die -2 ersetzen wir durch -1-1.

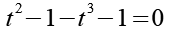      (Gl. 14)

Wir ersetzen 1 durch 12 bzw. 13.

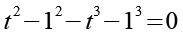      (Gl. 15)

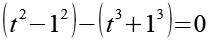      (Gl. 16)

Es gilt.

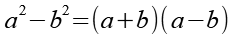      (Gl. 17)

Mit Hilfe von Gl. 17 erhalten wir.

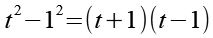      (Gl. 18)

Es gilt.

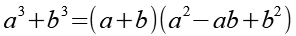      (Gl. 19)

Mit Hilfe von Gl. 19 erhalten wir.

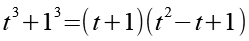      (Gl. 20)

Wir setzen Gl. 18 und Gl. 20 in Gl. 16 ein.

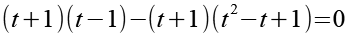      (Gl. 21)

Wir können (t+1) ausklammern.

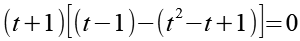      (Gl. 22)

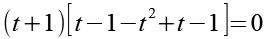      (Gl. 23)

Jede der beiden Klammern können wir separat gleich Null setzten.

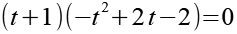      (Gl. 24)

Fangen wir mit der linken Klammer an.

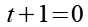      (Gl. 25)

Wir erhalten die erste Lösung für t.

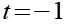      (Gl. 26)

Die zweite Klammer ist eine quadratische Gleichung.

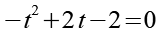      (Gl. 27)

Wir multiplizieren beide Seiten mit -1.

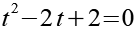      (Gl. 28)

Wir ersetzen die 2 durch +1+1.

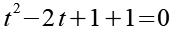      (Gl. 29)

Wir ersetzen die 1 durch 12.

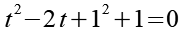      (Gl. 30)

Es gilt.

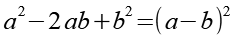      (Gl. 123)

Mit Hilfe von Gl. 123 erhalten wir aus Gl. 30.

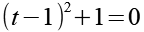      (Gl. 31)

Wir subtrahieren auf beiden Seiten -1.

      (Gl. 32)

Wir ziehen auf beiden Seiten die Wurzel.

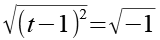      (Gl. 33)

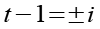      (Gl. 34)

Für t erhalten wir.

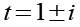      (Gl. 35)

Wir haben insgesamt 3 Lösungen für t.

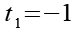      (Gl. 36)  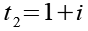     (Gl. 37)  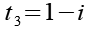     (Gl. 38)

Zuerst setzen wit t1 in Gl. 11 ein.

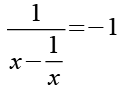      (Gl. 39)

Auf beiden Seiten bilden wir den Kehrwert.

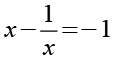      (Gl. 40)

Beide Seiten multilizieren wir mit x.

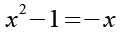      (Gl. 41)

Beide Seiten addieren wir x.

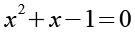      (Gl. 42)

Für die Lösung der quadratischen Gleichung gilt.

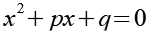      (Gl. 43)

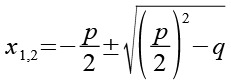      (Gl. 44)

Wir wenden Gl. 44 auf Gl. 42 an.

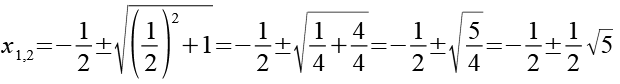      (Gl. 45)

Wir erhalten die ersten beiden Lösungen für Gl. 1.

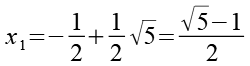      (Gl. 46)  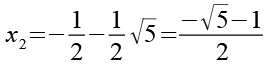     (Gl. 47)

Wir setzen t2 in Gl. 11 ein.

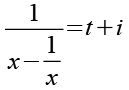      (Gl. 48)

Auf beiden Seiten bilden wir den Kehrwert.

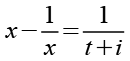      (Gl. 49)

Wir multiplizieren die rechte Seite mit (1-i)/(1-i).

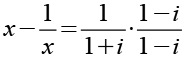      (Gl. 50)

Es gilt.

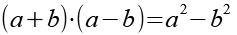      (Gl. 51)

Mit Hilfe von Gl. 51 erhalten wir aus Gl. 50.

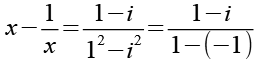      (Gl. 52)

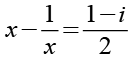      (Gl. 53)

Die linke Seite bringen wir auf den Hauptnenner x.

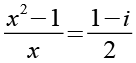      (Gl. 54)

Wir substituieren 1-i durch m.

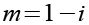      (Gl. 55)

Wir setzen Gl. 55 in Gl. 54 ein.

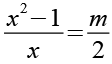      (Gl. 56)

Wir multiplizieren Gl. 56 über Kreuz.

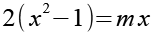      (Gl. 57)

Wir multiplizieren die Klammer aus.

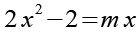      (Gl. 58)

Wir subtrahieren auf beiden Seiten m x.

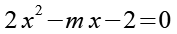      (Gl. 59)

Für die Lösung der quadratischen Gleichung gilt.

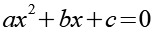      (Gl. 60)

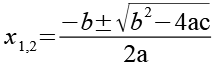      (Gl. 61)

Wir wenden Gl. 61 auf Gl. 59 an.

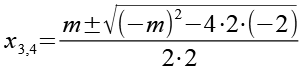      (Gl. 62)

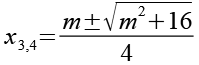      (Gl. 63)

Wir berechnen m2.

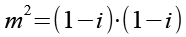      (Gl. 64)

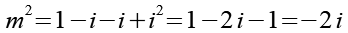      (Gl. 65)

Wir setzen Gl. 65 und Gl. 55 in Gl. 63 ein.

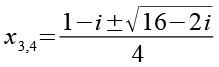      (Gl. 66)

Wir erhalten die nächsten beiden Lösungen für Gl. 1.

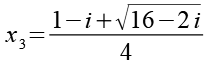      (Gl. 67)  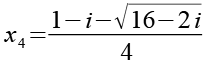     (Gl. 68)

Wir setzen t3 in Gl. 11 ein.

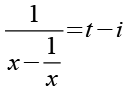      (Gl. 69)

Auf beiden Seiten bilden wir den Kehrwert.

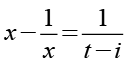      (Gl. 70)

Wir multiplizieren die rechte Seite mit (1+i)/(1+i).

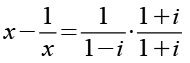      (Gl. 71)

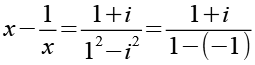      (Gl. 72)

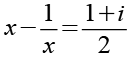      (Gl. 73)

Die linke Seite bringen wir auf den Hauptnenner x.

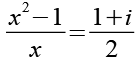      (Gl. 74)

Wir substituieren 1+i durch m.

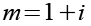      (Gl. 75)

Wir setzen Gl. 75 in Gl. 74 ein.

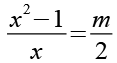      (Gl. 76)

Wir erhalten eine quadratische Gleichung.

      (Gl. 77)

Wir wenden Gl. 61 auf Gl. 77 an.

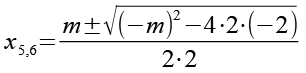      (Gl. 78)

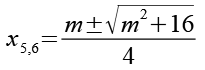      (Gl. 79)

Wir berechnen m2.

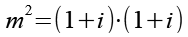      (Gl. 80)

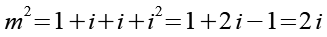      (Gl. 81)

Wir setzen Gl. 81 und Gl. 75 in Gl. 79 ein.

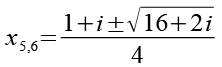      (Gl. 82)

Wir erhalten die letzten beiden Lösungen für Gl. 1.

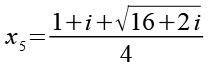      (Gl. 83)  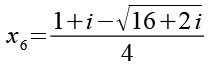     (Gl. 84)


Zur besseren Übersicht alle 6 Lösungsn incl. der Zahlenwerte.

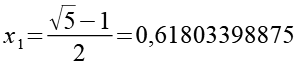      (Gl. 85)  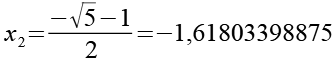          (Gl. 86)

      (Gl. 87)  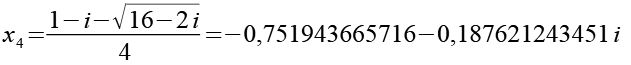     (Gl. 88)

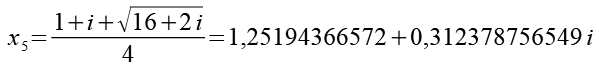      (Gl. 89)  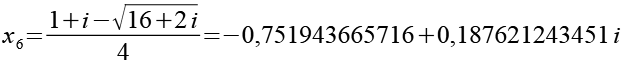     (Gl. 90)

x3 und x5 sowie x4 und x6 sind konjugiert komplex.


Anhang 1

      (Gl. 1)

Man kann Gl. 1 natürlich ganz normal ausmultiplizieren, das führt aber zu einem Polynom 6. Grades das nur nummerisch lösbar ist.

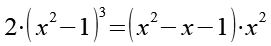      (Gl. 91)

Es gilt.

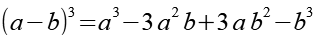      (Gl. 92)

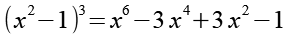      (Gl. 93)

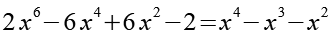      (Gl. 94)

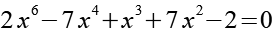      (Gl. 95)


Anhang 2

Die Lösungen x3 bis x6 sind komplexe Zahlen. Die imaginäre Einheit i kommt jeweils doppelt vor, es wäre natürlich schöner wenn das Ergebnis in der allgemeinen Form z=a+bi vorliegen würde. Dazu muss aber die Wurzel einer komplexen Zahl gezogen werden.

Für die Wurzel einer komplexen Zahl gilt.

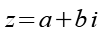      (Gl. 96)

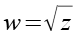      (Gl. 97)

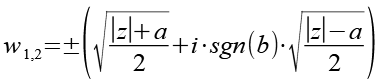      (Gl. 98)

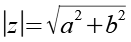      (Gl. 99)

Fangen wir mit x3 an.

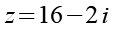      (Gl. 100)

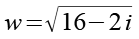      (Gl. 101)

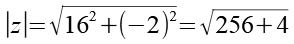      (Gl. 102)

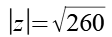      (Gl. 103)

Als Lösung von Gl. 101 erhalten wir.

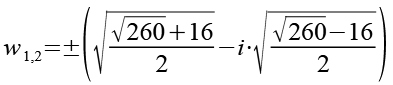      (Gl. 104)

Mit Hilde von Gl. 104 können wir x3 umformen.

      (Gl. 87)

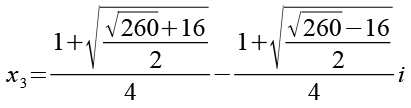      (Gl. 105)

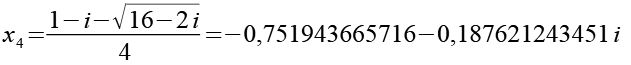      (Gl. 88)

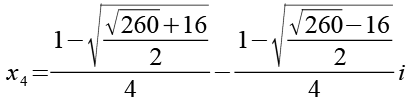      (Gl. 106)

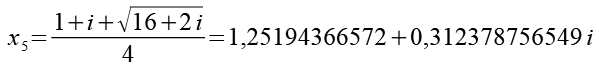      (Gl. 89)

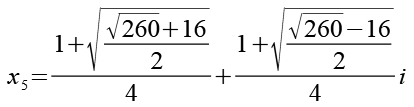      (Gl. 107)

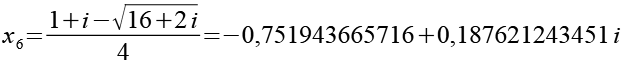      (Gl. 90)

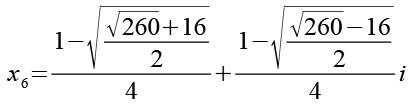      (Gl. 108)


Anhang 3

      (Gl. 1)

Zur Kontrolle setzen wir x1 in Gl. 1 ein, x1 läßt sich auch vom goldenen Schnitt ableiten.

Für den goldenen Schnitt gilt.

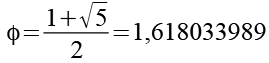      (Gl. 109)

Zur besseren Übersicht berechnen wir die einzelnen Teile von Gl. 1 separat.

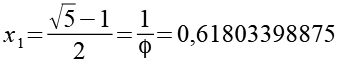      (Gl. 110)

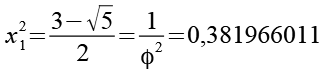      (Gl. 111)

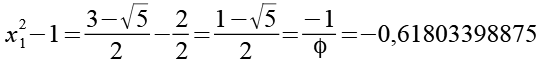      (Gl. 112)

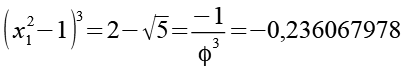      (Gl. 113)

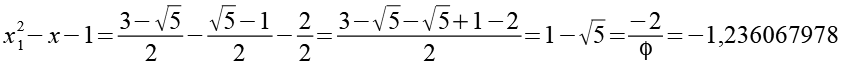      (Gl. 114)

Wir setzen Gl. 111, Gl. 113 und Gl. 114 in Gl. 1 ein.

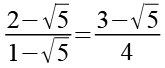      (Gl. 115)

Beide Seiten multiplizieren wir mit dem Nenner der linken Seite.

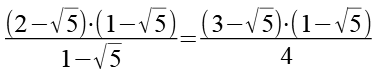      (Gl. 116)

Nach dem Kürzen erhalten wir.

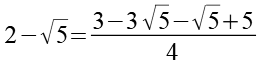      (Gl. 117)

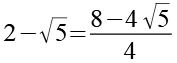      (Gl. 118)

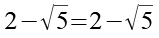      (Gl. 119)

Wir setzen Gl. 111, Gl. 113 und Gl. 114 in Gl. 1 ein, diesmal benutzen wir die Variante mit dem goldenen Schnitt Phi.

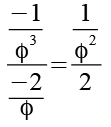      (Gl. 120)

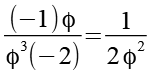      (Gl. 121)

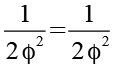      (Gl. 122)

[zurück] [Inhaltsverzeichnis] [vor]