Interessante Mathe Aufgaben
|
[zurück] | Interessante Mathe Aufgaben |
[vor] | |
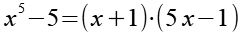(Gl. 1)
Zuerst multiplizieren wir die Klammern aus.
(Gl. 2)
(Gl. 3)
Auf beiden Seiten addieren wir 5.
(Gl. 4)
Auf beiden Seiten addieren wir x + 1.
(Gl. 5)
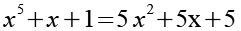(Gl. 6)
Auf der rechten Seite können wir 5 ausklammern und die Seiten vertauschen.
(Gl. 7)
(Gl. 8)
Auf der rechten Seite addieren wir -x2 + x2.
(Gl. 9)
Auf der rechten Seite können wir x2 ausklammern.
(Gl. 10)
Die 1 ersetzen wi durch 13.
(Gl. 11)
Es gilt:
(Gl. 12)
Mit Hilfe von Gl. 12 erhalten wir.
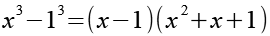(Gl. 13)
Gl. 13 setzen wir in Gl. 11 ein.
(Gl. 14)
Auf der rechten Seite klammern wir x2 + x + 1 aus.
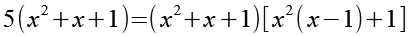(Gl. 15)
Auf der rechten Seite multipliziern wir x2(x - 1) aus.
(Gl. 16)
Auf beiden Seiten subtrahieren wir 5(x2 + x + 1).
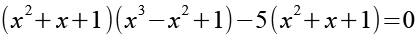(Gl. 17)
Die eckige Klammer können wir vereinfachen.
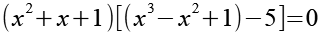(Gl. 18)
(Gl. 19)
Wir erhalten das Produkt zweier Polynome die wir separat gleich Null setzten können.
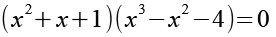(Gl. 20)
(Gl. 21)
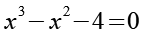(Gl. 28)
Fangen wir mit Gl. 21 an, einer quadratischen Gleichung.
(Gl. 21)
Es gilt:
(Gl. 22)
(Gl. 23)
Die Lösung ist trivial, mit Hilfe von Gl. 23 erhalten wir.
(Gl. 24)
Als Lösung von Gl. 20 erhalten wir zwei konjugiert komplexe Zahlen (x1 und x2).
(Gl. 25)
(Gl. 26)
(Gl. 27)
Jetzt machen wir mit Gl. 28 weiter.
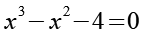(Gl. 28)
Für die -4 in Gleichung 28 können wir auch schreiben.
(Gl. 29)
Gl. 29 setzten wir in Gl. 28 ein.
(Gl. 30)
Die 8 und die 4 drücken wir durch Potenzen von 2 aus.
(Gl. 31)
(Gl. 32)
Es gilt:
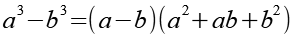(Gl. 33)
(Gl. 34)
Mit Hilfe von Gl. 33 erhalten wir.
(Gl. 35)
Mit Hilfe von Gl. 34 erhalten wir.
(Gl. 36)
Gl. 35 und Gl. 36 setzen wir in Gl. 32 ein.
(Gl. 37)
In Gl. 37 können wir (x - 2) ausklammern.
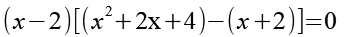(Gl. 38)
Die eckige Klammer können wir vereinfachen.
(Gl. 39)
Wir erhalten wieder ein Produkt zweier Polynome die wir separat gleich Null setzten können.
(Gl. 40)
Fangen wir mit der linken Klammer an.
(Gl. 41)
So erhalten wir die dritte Lösung für Gl. 1.
(Gl. 42)
Machen wir mit der rechten Klammer weiter, die Lösung ist trivial, siehe Gl. 23.
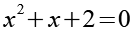(Gl. 43)
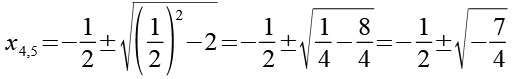(Gl. 44)
Als Lösung von Gl. 20 erhalten wir zwei konjugiert komplexe Zahlen (x4 und x5).
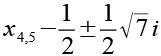(Gl. 45)
(Gl. 46)
(Gl. 47)
Gl. 1 hat 5 Lösungen, eine Reelle und 4 Komplexe.
Zur Kontrolle setzten wir die Lösung in Gl. 1 ein, fangen wir mit x3 an.
(Gl. 48)
(Gl. 49)
(Gl. 50)
Bei den komplexen Zahlen wird die Berechnung deutlich aufwändiger, wir machen mit x1 weiter und setzten sie in die rechte Seite von Gl. 1 ein.
(Gl. 50)
Für die Multiplikation komplexer Zahlen gilt:
(Gl. 51)
Mit Hilfe von Gl. 51 erhalten wir aus Gl. 50.
(Gl. 52)
Für die 5. Potenz einer komplexen Zahl gilt:
(Gl. 53)
Zuerst berechnen wir x15.
(Gl. 54)
Zur besseren Übersichtlichkeit berechnen wir den rellen und komplexen Teil separat.
(Gl. 55)
(Gl. 56)
(Gl. 57)
Gl. 57 setzen wir in die linke Seite von Gl. 1 ein
(Gl. 58)
Gl. 52 und Gl. 58 zeigen das gleich Ergebnis, damit ist x1 bewiesen.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |