Interessante Mathe Aufgaben

Interessante Mathe Aufgaben

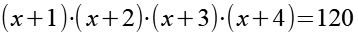(Gl. 1)

Vor dem Ausmultilplizieren stellen wir die Klammern etwas um.

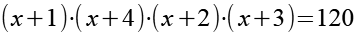(Gl. 1a)

(Gl. 2)

(Gl. 3)

In der zweiten Klammer ertsetzen wir die 6 durch 4 + 2.

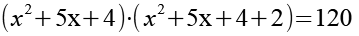(Gl. 4)

Wir substituieren x²+ 5a + 4 durch u.

(Gl. 5)

Gl. 5 setzen wir in Gl. 4 ein.

(Gl. 6)

(Gl. 7)

Wir erhalten eine quadratische Gleichung, zu einem alternativen Lösungsweg siehe Anhang.

(Gl. 8)

Für die quadratische Gleichung gilt:

(Gl. 9)

(Gl. 10)

(Gl. 11)

Für u erhalten wir zwei Lösungen.

(Gl. 12)

(Gl. 13)

u₁ setzen wir in Gl. 5 ein.

(Gl. 14)

Wir erhalten wieder eine quadratische Gleichung.

(Gl. 15)

(Gl. 16)

(Gl. 17)

(Gl. 18)

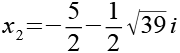(Gl. 19)

In zweiten Schritt setzen wir u₂ setzen wir in Gl. 5 ein.

(Gl. 20)

(Gl. 21)

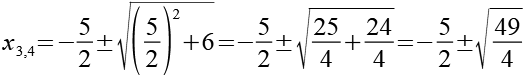(Gl. 22)

(Gl. 23)

(Gl. 24)

(Gl. 25)

Jetzt haben wir alle 4 Lösungen von Gl. 1, zwei Reelle und zwei Komplexe.

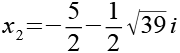
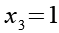
Zur Kontrolle setzen wir die Lösungen in Gl. 1 ein, fangen wir mit den reellen Lösungen an.

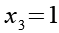
(Gl. 26)

(Gl. 27)

(Gl. 28)

Vor dem Ausmultilplizieren stellen wir die Klammern etwas um.

(Gl. 29)

Für die Multiplikation komplexer Zahlen gilt:

(Gl. 30)

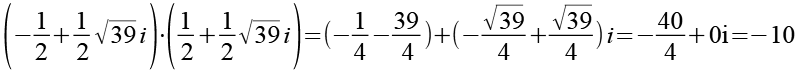(Gl. 31)

(Gl. 32)

Gl. 31 und Gl. 32 setzen wir in Gl. 29 ein.

(Gl. 33)

Als Ergebnbis erhalten wir wieder 120.

Anhang 1

Alternativer Lösungsweg für Gl. 8, die 2 ersetzen wir durch -10+12 und die -120 durch -10*12.

(Gl. 8)

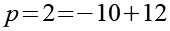(Gl. 34)

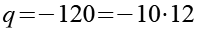(Gl. 35)

Gl. 34 und Gl. 35 setzen wir in Gl. 8 ein.

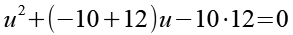(Gl. 36)

Wir multiplizieren die Klammer aus und stellen die Gleichung etwas um.

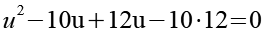(Gl. 37)

(Gl. 38)

Jetzt können wir einmal u und einmal -10 ausklammern.

(Gl. 39)

Jetzt können wir (u + 12) ausklammern.

(Gl. 40)

Beide Klammern setzten wir gleich Null und erhalten die beiden Lösungen der quadratischen Gleichung 8.

(Gl. 12)

(Gl. 13)

Anhang 2

Gl. 1 könnte man natürlich auch komplett ausmultiplizieren, das führt zu einem Polynom 4. Grades

(Gl. 41)

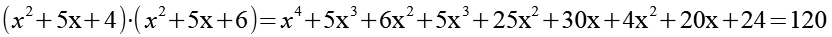(Gl. 42)

(Gl. 43)

(Gl. 44)

Gl. 44 ist lösbar aber dieser Weg ist deutlich komplizierter.

[Inhaltsverzeichnis]