| [zurück] | Gelenkviereck |
[vor] |
Ein ähnlicher Lösungsansatz ist in folgendem Buch beschrieben.
| R. Hartenberg, J. Denavit |
| Kinematic Synthesis Of Linkages |
| McGraw-Hill Book Company |
| Online |
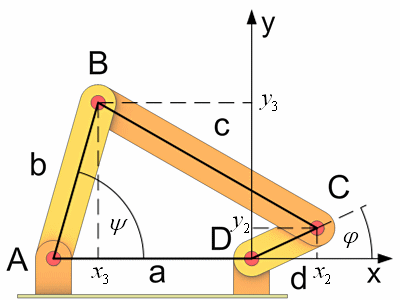
Die Maße des Gelenkvierecks habe ich vom Beispiel Kurbelschwinge übernommen.
| a = 5,5 | ||
| b = 4,5 | ||
| c = 7 | ||
| d = 2 | ||
| phi = 25° | ||
| psi = 74,01° |
Die Benennung der Stäbe und Punkte habe ich vom ersten Beispiel übernommen. Der Ursprung des Koordinatensystems liegt diesmal in Punkt D und nicht in Punkt A. Wichtig für die Berechnung sind die Koordinaten der Punkte B und C.
Für C gilt:
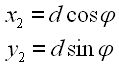 |
45 46 |
Für B gilt:
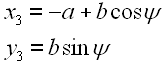 |
47 48 |
Daraus ergibt sich ein rechtwinkliges Dreieck auf das wir den Satz von Pythagoras anwenden können.
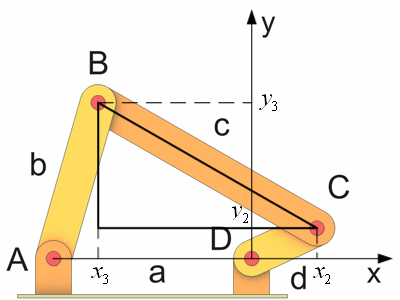
Für das Dreieck gilt.
| 49 |
Jetzt setzen wir Gl. 45 - Gl. 48 in Gl. 49 ein und erhalten Gl. 50.
| 50 |
Nach dem Ausmultiplizieren der Klammern und ein paar Umstellungen erhalten wir Gl. 51. Für den kompletten Lösungsweg siehe Anhang A7
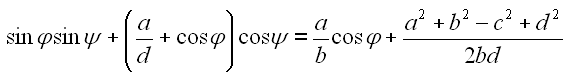 |
51 |
Durch Einführung der Konstanten A, B und C können wir Gl. 51 weiter vereinfachen.
| 52 | ||
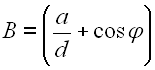 |
53 | |
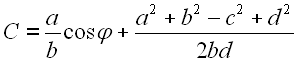 |
54 |
Jetzt setzen wir Gl. 52 - Gl. 54 in Gl. 51 ein und erhalten Gl. 55.
| 55 |
Wir ersetzen den Sinus und den Cosinus durch Gleichung B3 und B4.
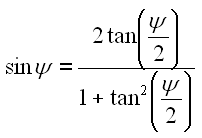 |
56 | |
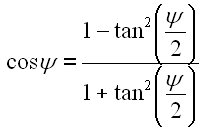 |
57 |
Jetzt setzen wir Gl. 56 und Gl. 57 in Gl. 55 ein und erhalten Gl. 58.
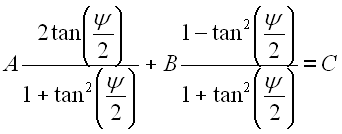 |
58 |
Gl. 58 können wir weiter vereinfachen und erhalten eine quadratische Gleichung. Für den kompletten Lösungsweg siehe Anhang A8
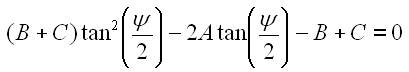 |
59 |
Nach B5 lösen wir die quadratischen Gleichung Gl. 59. Für den kompletten Lösungsweg siehe Anhang A9
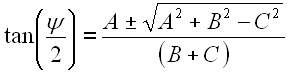 |
60 |
Um Gl. 60 zu überprüfen setzten wir die Zahlen unseres Beispiels ein (siehe Anhang A10).
| [zurück] | [Inhaltsverzeichnis] | [vor] |