| [zurück] | 7.2. Ikosaederstern |
[vor] |
 |
 |
| Isometrie | Dimetrie |
| Name | Ikosaederstern Great stellated dodecahedron |
| Anzahl Ecken | 32 |
| Anzahl Flächen | 60 gleichschenklige Dreiecke |

Der Ikosaederstern enthält 12 Pentagramme.

Der Ikosaederstern mit dem umhüllenden Dodekaeder.
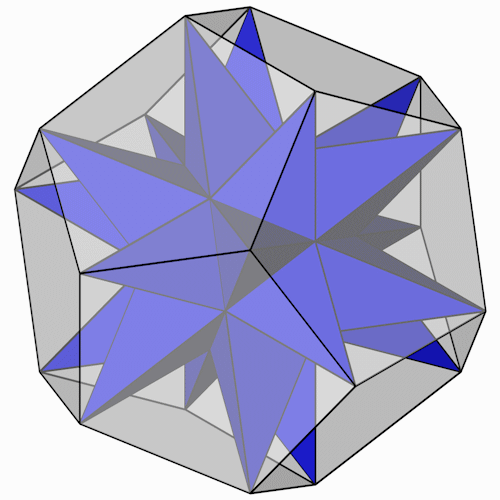

Der Ikosaederstern mit der Umkugel des Ikosaeders.

Der Ikosaederstern mit seiner Umkugel.

Für die Konstruktion des Ikosaedersterns gehen wir von einem Ikosaeder mit der Kantenlänge
aI=1 aus. Die Kanten des Ikosaeders werden über seine Ecken so verlängert dass sich jeweils
3 von ihnen in einem Punkt schneiden. So entstehen 20 Pyramiden die auf den Flächen des Ikosaeders
sitzen. Die Spitzen der pyramiden bilden die 20 Eckpunkte eines regelmäßigen Dodekaeders.
Da stellt sich die Frage welche Maße der Dodekaeder haben muss um mit dem
Ikosaeder die Eckpunkte des Ikosaedersterns zu bilden.
Den Ikosaederstern kann man auch durch 12 sich gegenseitig schneidenden Pentagramme darstellen. Betrachten wir so ein Pentagramm.
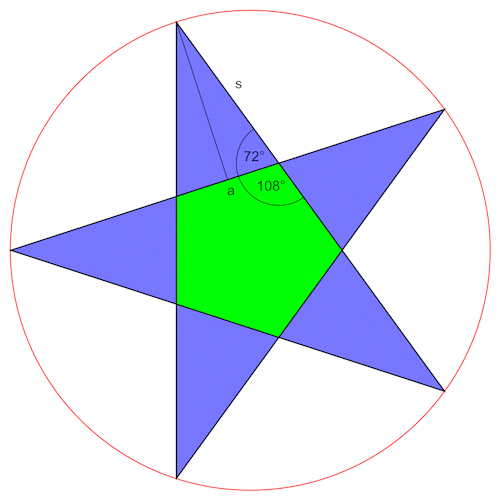 |
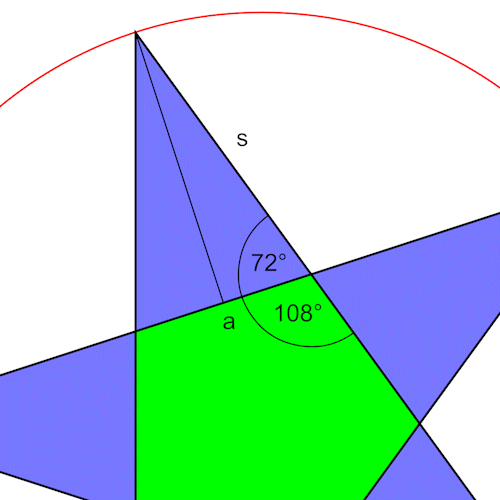 |
Die Seite s des Dreiecks ist gleichzeitig die Kante der Pyramide, sie läßt sich leicht über den Cosinus berechnen. Zur Vereinfachung benutzen wir den goldenen Schnitt phi.
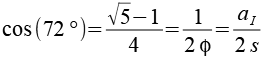

Die Höhe der Dreieckspyramide (hP) läßt sich aus der Kantenlänge s und dem Umkreisradius (ruDreieck) des Ikosaederdreiecks über den Pythagoras berechnen.

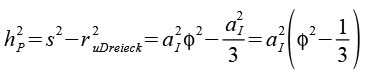

Der Ausdruck unter der Wurzel ist irgendwie unschön aber das läßt sich ändern. Es gilt
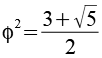
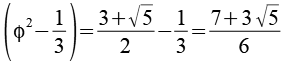
Es gilt
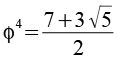
Daraus folgt
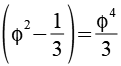
Für hP erhalten wir dann
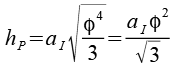
Wenn wir zur Höhe der Pyramide (hP) den Inkugelradius des Ikosaeders (riIkosaeder) addieren erhalten wir dem Umkugelradius des Dodeakaeders (ruD). Für riIkosaeder gilt
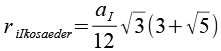
Mit
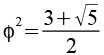
erhalten wir
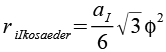
Der Umkugelradius des Dodeakaeders (ruD) ist

Der Umkugelradius des Dodeakaeders (ruD) wird normalerweise aus der Kantenlänge des Dodekaeders (aD) berechnet.

Diese Gleichung lösen wir nach aD auf.
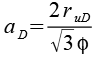
Jetzt setzen wir ruD ein.
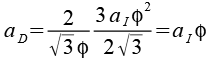
Für den Ikosaederstern muss die Kantenlänge des Dodekaeders um den Faktor Phi größer sein als die Kantenlänge des Ikosaeders.
| [zurück] | [Inhaltsverzeichnis] | [vor] |