10. Fermat Zahlen
|
[zurück] | 10. Fermat Zahlen |
[vor] | |
Eine Fermat Zahl ist wie folgt definiert:
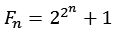
n ist eine natürliche Zahl. Nur die ersten 5 Fermat Zahlen sind Primzahlen.
| n | Fn |
|
0 1 2 3 4 5 6 7 8 |
3 5 17 257 65537 4294967297 18446744073709551617 340282366920938463463374607431768211457 115792089237316195423570985008687907853269984665640564039457584007913129639937 |
Fermat glaubte ursprünglich das alle Fermat Zahlen Primzahlen sind, das hat dann aber Leonhard Euler für F5 widerlegt.
F5 = 4294967297 = 641 * 6700417
F6 = 18446744073709551617 = 274177 * 67280421310721
Interessant ist auch die Binärdarstellung der Fermat Zahlen, das ergibt sich natürlich aus der Definition.
| n | Dezimal | Binär |
|
0 1 2 3 4 5 6 |
3 5 17 257 65537 4294967297 18446744073709551617 |
11 101 10001 100000001 10000000000000001 100000000000000000000000000000001 10000000000000000000000000000000000000000000000000000000000000001 |
Für die Teiler der Fermat Zahlen gilt.
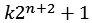
F5:
641 = 5 * 27 + 1 = 5 * 128 + 1
6700417 = 52347 * 27 + 1 = 52347 * 128 + 1
F6:
274177 = 1071 * 28 + 1 = 1071 * 256 + 1
67280421310721 = 262814145745 * 28 + 1 = 262814145745 * 256 + 1
Das gilt auch für die Fermat Primzahlen (für n > 1).
F2:
17 = 1 * 24 + 1 = 16 + 1
F3:
257 = 8 * 25 + 1 = 8 * 32 + 1
F4:
65537 = 1024 * 26 + 1 = 1024 * 64 + 1
Die Fermat Zahlen sich auch rekursiv berechnen.
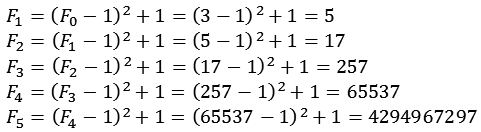
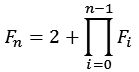
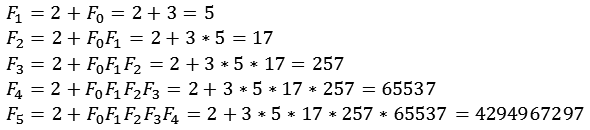
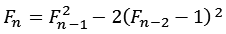
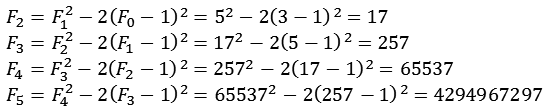
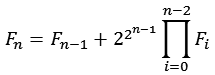
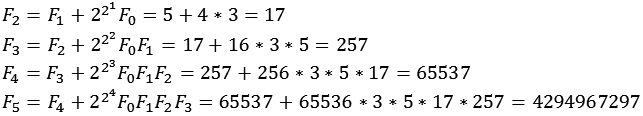
Alle Fermat Zahlen, bis auf F0 = 3 und F1 = 5, enden auf die Ziffer 7.
| n | Fn |
|
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
17 257 65537 4294967297 18446744073709551617 340282366920938463463374607431768211457 …85008687907853269984665640564039457584007913129639937 …90031858186486050853753882811946569946433649006084097 …10684586298239947245938479716304835356329624224137217 …35433229604645318478604952148193555853611059596230657 …91511131602920781738033436090243804708340403154190337 …81781469090806576468950587661997186505665475715792897 …18213934288295679717369943152460447027290669964066817 …82427627261046280168269958077541122668104633712377857 …72895337539755822087777506072339445587895905719156737 …80325362544275565838974676261850665812318570934173697 …03650107299993809500432559730753862605349934298300417 …68643349179648430125596209011369814364528226185773057 …48093374936943243527734573872009289119068940335579137 |
Die letzten beiden Ziffern sind 17, 37, 57 oder 97, dabei wiederholt sich die Reihenfolge 17, 57, 37 und 97.
Betrachten wir zusätzlich die drittletzte Ziffer.
17
| n | Fn |
|
2 6 10 14 18 |
17 18446744073709551617 …10684586298239947245938479716304835356329624224137217 …18213934288295679717369943152460447027290669964066817 …03650107299993809500432559730753862605349934298300417 |
Die drittletzte Ziffer ist 0, 2, 4, 6 und 8.
57
| n | Fn |
|
3 7 11 15 19 |
257 340282366920938463463374607431768211457 …35433229604645318478604952148193555853611059596230657 …82427627261046280168269958077541122668104633712377857 …68643349179648430125596209011369814364528226185773057 |
Die drittletzte Ziffer ist 0, 2, 4, 6 und 8.
37
| n | Fn |
|
4 8 12 16 20 |
65537 …85008687907853269984665640564039457584007913129639937 …91511131602920781738033436090243804708340403154190337 …72895337539755822087777506072339445587895905719156737 …48093374936943243527734573872009289119068940335579137 |
Die drittletzte Ziffer ist 1, 3, 5, 7 und 9.
97
| n | Fn |
|
5 9 13 17 |
4294967297 …90031858186486050853753882811946569946433649006084097 …81781469090806576468950587661997186505665475715792897 …80325362544275565838974676261850665812318570934173697 |
Die drittletzte Ziffer ist 0, 2, (4), 6 und 8.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |