Mathematische Spielereien

11. Mersenne Zahlen

Die Mersenne Zahlen sind wie folgt definiert:

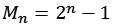
n	M_n	M_n binär
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40	0 1 3 7 15 31 63 127 255 511 1023 2047 4095 8191 16383 32767 65535 131071 262143 524287 1048575 2097151 4194303 8388607 16777215 33554431 67108863 134217727 268435455 536870911 1073741823 2147483647 4294967295 8589934591 17179869183 34359738367 68719476735 137438953471 274877906943 549755813887 1099511627775	1 11 111 1111 11111 111111 1111111 11111111 111111111 1111111111 11111111111 111111111111 1111111111111 11111111111111 111111111111111 1111111111111111 11111111111111111 111111111111111111 1111111111111111111 11111111111111111111 111111111111111111111 1111111111111111111111 11111111111111111111111 111111111111111111111111 1111111111111111111111111 11111111111111111111111111 111111111111111111111111111 1111111111111111111111111111 11111111111111111111111111111 111111111111111111111111111111 1111111111111111111111111111111 11111111111111111111111111111111 111111111111111111111111111111111 1111111111111111111111111111111111 11111111111111111111111111111111111 111111111111111111111111111111111111 1111111111111111111111111111111111111 11111111111111111111111111111111111111 111111111111111111111111111111111111111 1111111111111111111111111111111111111111

Auch die Darstellung im Dualsystem ist interessant, die Mersenne Zahl M_n bestehen aus n Einsen.

Einige Mersenne Zahlen sind Primzahlen, sie werden Mersenne-Primzahlen genannt.

n	M_n
2 3 5 7 13 17 19 31 61 89 107 127	3 7 31 127 8191 131071 524287 2147483647 2305843009213693951 618970019642690137449562111 162259276829213363391578010288127 170141183460469231731687303715884105727

Bei einer Mersenne Primzahl ist der Exponent n ebenfalls eine Primzahl. Aber nicht alle Mersenne Zahlen mit einer Primzahl als Exponent sind Primzahlen.

Ist r ein Teiler von n, dann ist M_r auch ein Teiler von M_n. Ein paar Beispiele

n = 6 = 2 * 3
M₂ = 3
M₃ = 7
M₆ = 63 = 3 * 3 * 7

n = 8 = 2 * 4
M₂ = 3
M₄ = 15
M₈ = 255 = 3 * 5 * 17 = 15 * 17

n = 14 = 2 * 7
M₂ = 3
M₇ = 127
M₁₄ = 16383 = 3 * 43 * 127

n = 20 = 4 * 5
M₄ = 15
M₅ = 31
M₂₀ = 1048575 = 5 * 11 * 15 * 31 * 41

Ist n eine gerade Zahl und n + 1 eine Primzahl, so ist n + 1 ein Teiler von M_n. Ein paar Beispiele.

n = 6
n + 1 = 7
M₆ = 63 = 3 * 3 * 7

n = 12
n + 1 = 13
M₁₂ = 4095 = 3 * 3 * 5 * 7 * 13

n = 22
n + 1 = 23
M₂₂ = 4194303 = 3 * 23 * 89 * 683

n = 30
n + 1 = 31
M₃₀ = 1073741823 = 3 * 3 * 7 * 11 * 31 * 151 * 331

n = 36
n + 1 = 37
M₃₆ = 68719476735 = 3 * 3 * 3 * 5 * 7 * 13 * 19 * 37 * 73 * 109

Ist n = 2^m mit m > 0, dann ist M_n das Produkt der Fermat Zahlen F₀ bis F_m-1.

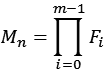
Ein paar Beispiele.

n = 4 = 2²
M₄ = 15 = F₀ * F₁ = 3 * 5 = 15

n = 8 = 2³
M₈ = 255 = F₀ * F₁ * F₂ = 3 * 5 * 17 = 255

n = 16 = 2⁴
M₁₆ = 65535 = F₀ * F₁ * F₂ * F₃ = 3 * 5 * 17 * 257 = 65535

n = 32 = 2⁵
M₃₂ = 4294967295 = F₀ * F₁ * F₂ * F₃ * F₄ = 3 * 5 * 17 * 257 * 65537 = 4294967295

Von den Mersenne-Primzahlen lassen sich die vollkommenen Zahlen (auch perfekte Zahlen) ableiten.
Eine natürliche Zahl n ist dann eine vollkommene Zahl, wenn sie gleich der Summe aller ihrer (positiven) Teiler außer sich selbst ist. Es gilt:

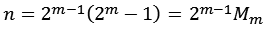
Wenn M_m eine Primzahl ist dann ist n eine vollkommene Zahl. Ein paar Beispiele.

m = 2
n = 2¹ M₂ = 2 * 3 = 6 = 1 + 2 + 3

m = 3
n = 2² M₃ = 4 * 7 = 28 = 1 + 2 + 4 + 7 + 14

m = 5
n = 2⁴ M₅ = 16 * 31 = 496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248

m = 7
n = 2⁶ M₇ = 64 * 127 = 8128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064

m = 13
n = 2¹² M₁₃ = 4096 * 8191 = 33550336

m = 17
n = 2¹⁶ M₁₇ = 65536 * 131071 = 8589869056

m = 19
n = 2¹⁸ M₁₉ = 262144 * 524287 = 137438691328

m = 31
n = 2³⁰ M₃₁ = 1073741824 * 2147483647 = 2305843008139952128

m = 61
n = 2⁶⁰ M₆₁ = 1152921504606846976 * 2305843009213693951 = 2658455991569831744654692615953842176

Die perfekten Zahlen enden immer auf 6 oder 8 (bzw. 28).

[zurück]

[Inhaltsverzeichnis]

[vor]