14. Schnapszahlen
|
[zurück] | 14. Schnapszahlen |
[vor] | |
Mit den Schnapszahlen hatte ich mich schon kurz bei den Kaprekar Zahlen befasst und ihnen jetzt eine eigene Seite gewidmet. Die Schnapszahlen sind wie folgt definiert, d ist die verwendete Ziffer und n ist die Anzanl der Stellen.
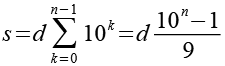
Z.B. für d = 3 und n = 4.
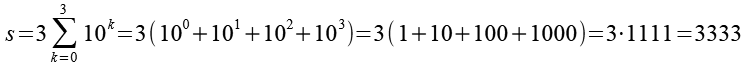
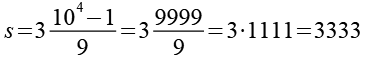
Alle dreistelligen Schnapszahlen sind durch 37 teilbar.
| Schnapszahl | Primfaktorzerlegung | |
| 111 222 333 444 555 666 777 888 999 |
3·37 2·3·37 3·3·37 2·2·3·37 3·5·37 2·3·3·37 3·7·37 2·2·2·3·37 3·3·3·37 |
3·37 6·37 9·37 12·37 15·37 18·37 21·37 24·37 27·37 |
Alle Schnapszahlen der gleichen Länge haben natürlich auch den größten Primfaktor gemeinsam. Bei dreistelligen Schnapszahlen ist es die 37, bei vierstelligen Schnapszahlen ist es die 101. Für längere Schnapszahlen gilt.
| Stellen | größter Primfaktor | Kehrwert größter Primfaktor | |
| 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
37 101 271 37 4649 137 333667 9091 513239 9901 265371653 909091 2906161 5882353 5363222357 333667 1111111111111111111 27961 10838689 513239 11111111111111111111111 99990001 182521213001 1058313049 440334654777631 121499449 77843839397 2906161 |
0.02702702702702702702702702702702702702702702702702702702702702702702702702702702702702702702702702703 0.00990099009900990099009900990099009900990099009900990099009900990099009900990099009900990099009900990 0.00369003690036900369003690036900369003690036900369003690036900369003690036900369003690036900369003690 0.02702702702702702702702702702702702702702702702702702702702702702702702702702702702702702702702702703 0.00021510002151000215100021510002151000215100021510002151000215100021510002151000215100021510002151000 0.00729927007299270072992700729927007299270072992700729927007299270072992700729927007299270072992700729 0.00000299700000299700000299700000299700000299700000299700000299700000299700000299700000299700000299700 0.00010999890001099989000109998900010999890001099989000109998900010999890001099989000109998900010999890 0.00000194841000001948410000019484100000194841000001948410000019484100000194841000001948410000019484100 0.00010099989900010099989900010099989900010099989900010099989900010099989900010099989900010099989900010 0.00000000376830000000037683000000003768300000000376830000000037683000000003768300000000376830000000037 0.00000109999989000001099999890000010999998900000109999989000001099999890000010999998900000109999989000 0.00000034409655900000034409655900000034409655900000034409655900000034409655900000034409655900000034409 0.00000016999999830000001699999983000000169999998300000016999999830000001699999983000000169999998300000 0.00000000018645507000000000186455070000000001864550700000000018645507000000000186455070000000001864550 0.00000299700000299700000299700000299700000299700000299700000299700000299700000299700000299700000299700 0.00000000000000000090000000000000000009000000000000000000900000000000000000090000000000000000009000000 0.00003576409999642359000035764099996423590000357640999964235900003576409999642359000035764099996423590 0.00000009226208077379100000009226208077379100000009226208077379100000009226208077379100000009226208077 0.00000194841000001948410000019484100000194841000001948410000019484100000194841000001948410000019484100 0.00000000000000000000009000000000000000000000090000000000000000000000900000000000000000000009000000000 0.00000001000099999998999900000001000099999998999900000001000099999998999900000001000099999998999900000 0.00000000000547881522129990000000000054788152212999000000000005478815221299900000000000547881522129990 0.00000000094489999999990551000000000944899999999905510000000009448999999999055100000000094489999999990 0.00000000000000227099999772900000000000000227099999772900000000000000227099999772900000000000000227099 0.00000000823048999999991769510000000082304899999999176951000000008230489999999917695100000000823048999 0.00000000001284623173453773267000000000012846231734537732670000000000128462317345377326700000000001284 0.00000034409655900000034409655900000034409655900000034409655900000034409655900000034409655900000034409 |
27 = 3·3·3 99 = 3·3·11 369 = 3·3·41 27 = 3·3·3 2151 = 3·3·239 729927 = 3·3·11·73·101 2997 = 3·3·3·3·37 1099989 = 3·3·11·41·271 194841 = 3·3·21649 100999899 = 3·3·3·7·11·13·37·101 37683 = 3·3·53·79 109999989 = 3·3·11·239·4649 344096559 = 3·3·3·31·37·41·271 1699999983 = 3·3·11·17·73·101·137 18645507 = 3·3·2071723 2997 = 3·3·3·3·37 9 = 3·3 3576409999642359 = 3·3·11·41·101·271·3541·9091 92262080773791 = 3·3·3·37·43·239·1933·4649 194841 = 3·3·21649 9 = 3·3 10000999999989999 = 3·3·3·7·11·13·37·73·101·137·9901 54788152212999 = 3·3·41·271·21401·25601 94489999999990551 = 3·3·11·53·79·859·265371653 2270999997729 = 3·3·3·3·3·37·757·333667 82304899999999176951 = 3·3·11·29·101·239·281·4649·909091 1284623173453773267 = 3·3·3191·16763·43037·62003 344096559 = 3·3·3·31·37·41·271 |
Schauen wir uns den Kehrwert genauer an und bilden wieder die Primfaktorzerlegng der Perioden. Allen gemeinsam ist der Faktor 3·3, vielleicht ist das trivial, ich fand das interessant..
https://www.math.kyoto-u.ac.jp/~yamasaki/repunit.dat.htmlDie Quadrate der Schnapszahlen.
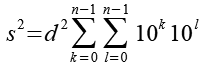
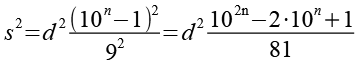
Z.B. für d = 3 und n = 4.
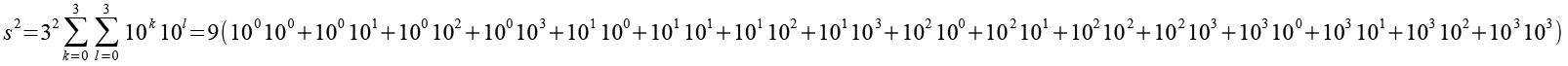
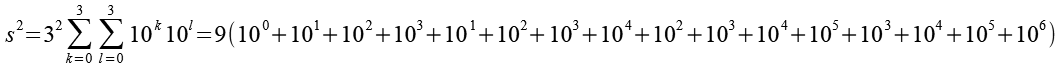
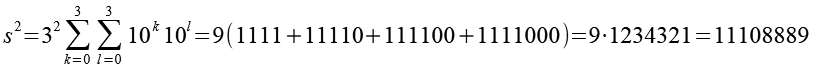
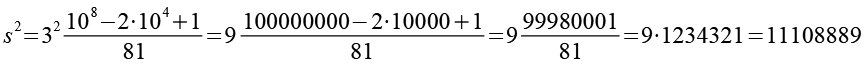
Interessant sind die sich wiederholenden Sequenzen (Fett gedruckt) der Quadrate der Schnapszahlen, bei Schnapszahlen mit der Ziffer 3, 6 und 9 gibt es sie nicht.
| n | Zahl | Quadrat |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
11 111 1111 11111 111111 1111111 11111111 111111111 1111111111 11111111111 111111111111 1111111111111 11111111111111 111111111111111 1111111111111111 11111111111111111 111111111111111111 1111111111111111111 11111111111111111111 111111111111111111111 1111111111111111111111 11111111111111111111111 111111111111111111111111 1111111111111111111111111 11111111111111111111111111 111111111111111111111111111 1111111111111111111111111111 11111111111111111111111111111 111111111111111111111111111111 |
121 12321 1234321 123454321 12345654321 1234567654321 123456787654321 12345678987654321 1234567900987654321 123456790120987654321 12345679012320987654321 1234567901234320987654321 123456790123454320987654321 12345679012345654320987654321 1234567901234567654320987654321 123456790123456787654320987654321 12345679012345678987654320987654321 1234567901234567900987654320987654321 123456790123456790120987654320987654321 12345679012345679012320987654320987654321 1234567901234567901234320987654320987654321 123456790123456790123454320987654320987654321 12345679012345679012345654320987654320987654321 1234567901234567901234567654320987654320987654321 123456790123456790123456787654320987654320987654321 12345679012345679012345678987654320987654320987654321 1234567901234567901234567900987654320987654320987654321 123456790123456790123456790120987654320987654320987654321 12345679012345679012345679012320987654320987654320987654321 |
Die beiden Sequenzen sind 123456790 und 987654320.
| n | Zahl | Quadrat |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
22 222 2222 22222 222222 2222222 22222222 222222222 2222222222 22222222222 222222222222 2222222222222 22222222222222 222222222222222 2222222222222222 22222222222222222 222222222222222222 2222222222222222222 22222222222222222222 222222222222222222222 2222222222222222222222 22222222222222222222222 222222222222222222222222 2222222222222222222222222 22222222222222222222222222 222222222222222222222222222 2222222222222222222222222222 22222222222222222222222222222 222222222222222222222222222222 |
484 49284 4937284 493817284 49382617284 4938270617284 493827150617284 49382715950617284 4938271603950617284 493827160483950617284 49382716049283950617284 4938271604937283950617284 493827160493817283950617284 49382716049382617283950617284 4938271604938270617283950617284 493827160493827150617283950617284 49382716049382715950617283950617284 4938271604938271603950617283950617284 493827160493827160483950617283950617284 49382716049382716049283950617283950617284 4938271604938271604937283950617283950617284 493827160493827160493817283950617283950617284 49382716049382716049382617283950617283950617284 4938271604938271604938270617283950617283950617284 493827160493827160493827150617283950617283950617284 49382716049382716049382715950617283950617283950617284 4938271604938271604938271603950617283950617283950617284 493827160493827160493827160483950617283950617283950617284 49382716049382716049382716049283950617283950617283950617284 |
Die beiden Sequenzen sind 493827160 und 172839506.
| n | Zahl | Quadrat |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
33 333 3333 33333 333333 3333333 33333333 333333333 3333333333 33333333333 333333333333 3333333333333 33333333333333 333333333333333 3333333333333333 33333333333333333 333333333333333333 3333333333333333333 33333333333333333333 333333333333333333333 3333333333333333333333 33333333333333333333333 333333333333333333333333 3333333333333333333333333 33333333333333333333333333 333333333333333333333333333 3333333333333333333333333333 33333333333333333333333333333 333333333333333333333333333333 |
1089 110889 11108889 1111088889 111110888889 11111108888889 1111111088888889 111111110888888889 11111111108888888889 1111111111088888888889 111111111110888888888889 11111111111108888888888889 1111111111111088888888888889 111111111111110888888888888889 11111111111111108888888888888889 1111111111111111088888888888888889 111111111111111110888888888888888889 11111111111111111108888888888888888889 1111111111111111111088888888888888888889 111111111111111111110888888888888888888889 11111111111111111111108888888888888888888889 1111111111111111111111088888888888888888888889 111111111111111111111110888888888888888888888889 11111111111111111111111108888888888888888888888889 1111111111111111111111111088888888888888888888888889 111111111111111111111111110888888888888888888888888889 11111111111111111111111111108888888888888888888888888889 1111111111111111111111111111088888888888888888888888888889 111111111111111111111111111110888888888888888888888888888889 |
| n | Zahl | Quadrat |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
44 444 4444 44444 444444 4444444 44444444 444444444 4444444444 44444444444 444444444444 4444444444444 44444444444444 444444444444444 4444444444444444 44444444444444444 444444444444444444 4444444444444444444 44444444444444444444 444444444444444444444 4444444444444444444444 44444444444444444444444 444444444444444444444444 4444444444444444444444444 44444444444444444444444444 444444444444444444444444444 4444444444444444444444444444 44444444444444444444444444444 444444444444444444444444444444 |
1936 197136 19749136 1975269136 197530469136 19753082469136 1975308602469136 197530863802469136 19753086415802469136 1975308641935802469136 197530864197135802469136 19753086419749135802469136 1975308641975269135802469136 197530864197530469135802469136 19753086419753082469135802469136 1975308641975308602469135802469136 197530864197530863802469135802469136 19753086419753086415802469135802469136 1975308641975308641935802469135802469136 197530864197530864197135802469135802469136 19753086419753086419749135802469135802469136 1975308641975308641975269135802469135802469136 197530864197530864197530469135802469135802469136 19753086419753086419753082469135802469135802469136 1975308641975308641975308602469135802469135802469136 197530864197530864197530863802469135802469135802469136 19753086419753086419753086415802469135802469135802469136 1975308641975308641975308641935802469135802469135802469136 197530864197530864197530864197135802469135802469135802469136 |
Die beiden Sequenzen sind 197530864 und 246913580.
| n | Zahl | Quadrat |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
55 555 5555 55555 555555 5555555 55555555 555555555 5555555555 55555555555 555555555555 5555555555555 55555555555555 555555555555555 5555555555555555 55555555555555555 555555555555555555 5555555555555555555 55555555555555555555 555555555555555555555 5555555555555555555555 55555555555555555555555 555555555555555555555555 5555555555555555555555555 55555555555555555555555555 555555555555555555555555555 5555555555555555555555555555 55555555555555555555555555555 555555555555555555555555555555 |
3025 308025 30858025 3086358025 308641358025 30864191358025 3086419691358025 308641974691358025 30864197524691358025 3086419753024691358025 308641975308024691358025 30864197530858024691358025 3086419753086358024691358025 308641975308641358024691358025 30864197530864191358024691358025 3086419753086419691358024691358025 308641975308641974691358024691358025 30864197530864197524691358024691358025 3086419753086419753024691358024691358025 308641975308641975308024691358024691358025 30864197530864197530858024691358024691358025 3086419753086419753086358024691358024691358025 308641975308641975308641358024691358024691358025 30864197530864197530864191358024691358024691358025 3086419753086419753086419691358024691358024691358025 308641975308641975308641974691358024691358024691358025 30864197530864197530864197524691358024691358024691358025 3086419753086419753086419753024691358024691358024691358025 308641975308641975308641975308024691358024691358024691358025 |
Die beiden Sequenzen sind 308641975 und 246913580.
| n | Zahl | Quadrat |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
66 666 6666 66666 666666 6666666 66666666 666666666 6666666666 66666666666 666666666666 6666666666666 66666666666666 666666666666666 6666666666666666 66666666666666666 666666666666666666 6666666666666666666 66666666666666666666 666666666666666666666 6666666666666666666666 66666666666666666666666 666666666666666666666666 6666666666666666666666666 66666666666666666666666666 666666666666666666666666666 6666666666666666666666666666 66666666666666666666666666666 666666666666666666666666666666 |
4356 443556 44435556 4444355556 444443555556 44444435555556 4444444355555556 444444443555555556 44444444435555555556 4444444444355555555556 444444444443555555555556 44444444444435555555555556 4444444444444355555555555556 444444444444443555555555555556 44444444444444435555555555555556 4444444444444444355555555555555556 444444444444444443555555555555555556 44444444444444444435555555555555555556 4444444444444444444355555555555555555556 444444444444444444443555555555555555555556 44444444444444444444435555555555555555555556 4444444444444444444444355555555555555555555556 444444444444444444444443555555555555555555555556 44444444444444444444444435555555555555555555555556 4444444444444444444444444355555555555555555555555556 444444444444444444444444443555555555555555555555555556 44444444444444444444444444435555555555555555555555555556 4444444444444444444444444444355555555555555555555555555556 444444444444444444444444444443555555555555555555555555555556 |
| n | Zahl | Quadrat |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
77 777 7777 77777 777777 7777777 77777777 777777777 7777777777 77777777777 777777777777 7777777777777 77777777777777 777777777777777 7777777777777777 77777777777777777 777777777777777777 7777777777777777777 77777777777777777777 777777777777777777777 7777777777777777777777 77777777777777777777777 777777777777777777777777 7777777777777777777777777 77777777777777777777777777 777777777777777777777777777 7777777777777777777777777777 77777777777777777777777777777 777777777777777777777777777777 |
5929 603729 60481729 6049261729 604937061729 60493815061729 6049382595061729 604938270395061729 60493827148395061729 6049382715928395061729 604938271603728395061729 60493827160481728395061729 6049382716049261728395061729 604938271604937061728395061729 60493827160493815061728395061729 6049382716049382595061728395061729 604938271604938270395061728395061729 60493827160493827148395061728395061729 6049382716049382715928395061728395061729 604938271604938271603728395061728395061729 60493827160493827160481728395061728395061729 6049382716049382716049261728395061728395061729 604938271604938271604937061728395061728395061729 60493827160493827160493815061728395061728395061729 6049382716049382716049382595061728395061728395061729 604938271604938271604938270395061728395061728395061729 60493827160493827160493827148395061728395061728395061729 6049382716049382716049382715928395061728395061728395061729 604938271604938271604938271603728395061728395061728395061729 |
Die beiden Sequenzen sind 604938271 und 172839506.
| n | Zahl | Quadrat |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
88 888 8888 88888 888888 8888888 88888888 888888888 8888888888 88888888888 888888888888 8888888888888 88888888888888 888888888888888 8888888888888888 88888888888888888 888888888888888888 8888888888888888888 88888888888888888888 888888888888888888888 8888888888888888888888 88888888888888888888888 888888888888888888888888 8888888888888888888888888 88888888888888888888888888 888888888888888888888888888 8888888888888888888888888888 88888888888888888888888888888 888888888888888888888888888888 |
7744 788544 78996544 7901076544 790121876544 79012329876544 7901234409876544 790123455209876544 79012345663209876544 7901234567743209876544 790123456788543209876544 79012345678996543209876544 7901234567901076543209876544 790123456790121876543209876544 79012345679012329876543209876544 7901234567901234409876543209876544 790123456790123455209876543209876544 79012345679012345663209876543209876544 7901234567901234567743209876543209876544 790123456790123456788543209876543209876544 79012345679012345678996543209876543209876544 7901234567901234567901076543209876543209876544 790123456790123456790121876543209876543209876544 79012345679012345679012329876543209876543209876544 7901234567901234567901234409876543209876543209876544 790123456790123456790123455209876543209876543209876544 79012345679012345679012345663209876543209876543209876544 7901234567901234567901234567743209876543209876543209876544 790123456790123456790123456788543209876543209876543209876544 |
Die beiden Sequenzen sind 790123456 und 987654320.
| n | Zahl | Quadrat |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
99 999 9999 99999 999999 9999999 99999999 999999999 9999999999 99999999999 999999999999 9999999999999 99999999999999 999999999999999 9999999999999999 99999999999999999 999999999999999999 9999999999999999999 99999999999999999999 999999999999999999999 9999999999999999999999 99999999999999999999999 999999999999999999999999 9999999999999999999999999 99999999999999999999999999 999999999999999999999999999 9999999999999999999999999999 99999999999999999999999999999 999999999999999999999999999999 |
9801 998001 99980001 9999800001 999998000001 99999980000001 9999999800000001 999999998000000001 99999999980000000001 9999999999800000000001 999999999998000000000001 99999999999980000000000001 9999999999999800000000000001 999999999999998000000000000001 99999999999999980000000000000001 9999999999999999800000000000000001 999999999999999998000000000000000001 99999999999999999980000000000000000001 9999999999999999999800000000000000000001 999999999999999999998000000000000000000001 99999999999999999999980000000000000000000001 9999999999999999999999800000000000000000000001 999999999999999999999998000000000000000000000001 99999999999999999999999980000000000000000000000001 9999999999999999999999999800000000000000000000000001 999999999999999999999999998000000000000000000000000001 99999999999999999999999999980000000000000000000000000001 9999999999999999999999999999800000000000000000000000000001 999999999999999999999999999998000000000000000000000000000001 |
Für jede Schnapszahl mit der Ziffer 1, 2, 4, 5, 7 und 8 gibt es im Quadrat zwei Sequenzen die sich wiederholen wenn die Zahl ausreichend groß ist. Diese Sequenzen haben in ihrer Primfaktorzerlegung verblüffende Gemeinsamkeiten.
| Basis | Sequenz | Primfaktorzerlegung | |
| 1 | 123456790 987654320 |
2 · 5 · 37 · 333667 2 · 2 · 2 · 2 · 5 · 37 · 333667 |
12 · 2 · 5 · 37 · 333667 1 · 2 · 2 · 2 · 2 · 5 · 37 · 333667 |
| 2 | 493827160 172839506 |
2 · 2 · 2 · 5 · 37 · 333667 2 · 7 · 37 · 333667 |
22 · 2 · 5 · 37 · 333667 2 · 7 · 37 · 333667 |
| 4 | 197530864 246913580 |
2 · 2 · 2 · 2 · 37 · 333667 2 · 2 · 5 · 37 · 333667 |
42 · 37 · 333667 4 · 5 · 37 · 333667 |
| 5 | 308641975 246913580 |
5 · 5 · 37 · 333667 2 · 2 · 5 · 37 · 333667 |
52 · 37 · 333667 5 · 2 · 2 · 37 · 333667 |
| 7 | 604938271 172839506 |
7 · 7 · 37 · 333667 2 · 7 · 37 · 333667 |
72 · 37 · 333667 7 · 2 · 37 · 333667 |
| 8 | 790123456 987654320 |
2 · 2 · 2 · 2 · 2 · 2 · 37 · 333667 2 · 2 · 2 · 2 · 5 · 37 · 333667 |
82 · 37 · 333667 8 · 2 · 5 · 37 · 333667 |
Alle Sequenzen enthalten die Faktoren 37 und 333667, beide Zahlen sind ähnlich aufgebaut. Wenn man die Zahlen als "ab" in der Mitte trennt kann man b aus a berechnen.
b = 2·a + 1
7 = 2·3 + 1
667 = 2·333 + 1
Auch die Basis der Schnapszahl taucht in der Primfaktorzerlegung der Sequenzen auf wenn man die entsprechenden Zahlen kombiniert. Die erste Sequenz enthält die Basis als Quadrat, die zweite Sequenz als einfache Zahl.
Zwei Sequenzen tauchen doppelt auf, 172839506 und 987654320.
Vier Sequenzen leiten sich von der ersten Sequenz ab.
123456790 = 1 · 123456790
246913580 = 2 · 123456790
493827160 = 4 · 123456790
987654320 = 8 · 123456790
Für die Sequenzen s1 und s2 einer Schnapszahl der Basis d gilt.
s1 = d2·k·37·333667
s2 = d·k·37·333667
k ist eine Konstante [2, 4, 5, 7, 10, 16].
Wie sieht das bei der 3. Potenz aus?
| n | Zahl | 3. Potenz |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
11 111 1111 11111 111111 1111111 11111111 111111111 1111111111 11111111111 111111111111 1111111111111 11111111111111 111111111111111 1111111111111111 11111111111111111 111111111111111111 1111111111111111111 11111111111111111111 111111111111111111111 1111111111111111111111 11111111111111111111111 111111111111111111111111 1111111111111111111111111 11111111111111111111111111 111111111111111111111111111 1111111111111111111111111111 11111111111111111111111111111 111111111111111111111111111111 |
1331 1367631 1371330631 1371700960631 1371737997260631 1371741700960260631 1371742071330590260631 1371742108367626890260631 1371742112071330589890260631 1371742112441700960219890260631 1371742112478737997256519890260631 1371742112482441700960219519890260631 1371742112482812071330589849519890260631 1371742112482849108367626886149519890260631 1371742112482852812071330589849149519890260631 1371742112482853182441700960219479149519890260631 1371742112482853219478737997256515779149519890260631 1371742112482853223182441700960219478779149519890260631 1371742112482853223552812071330589849108779149519890260631 1371742112482853223589849108367626886145408779149519890260631 1371742112482853223593552812071330589849108408779149519890260631 1371742112482853223593923182441700960219478738408779149519890260631 1371742112482853223593960219478737997256515775038408779149519890260631 1371742112482853223593963923182441700960219478738038408779149519890260631 1371742112482853223593964293552812071330589849108368038408779149519890260631 1371742112482853223593964330589849108367626886145404668038408779149519890260631 1371742112482853223593964334293552812071330589849108367668038408779149519890260631 1371742112482853223593964334663923182441700960219478737997668038408779149519890260631 1371742112482853223593964334700960219478737997256515775034297668038408779149519890260631 |
| n | Zahl | 3. Potenz |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
22 222 2222 22222 222222 2222222 22222222 222222222 2222222222 22222222222 222222222222 2222222222222 22222222222222 222222222222222 2222222222222222 22222222222222222 222222222222222222 2222222222222222222 22222222222222222222 222222222222222222222 2222222222222222222222 22222222222222222222222 222222222222222222222222 2222222222222222222222222 22222222222222222222222222 222222222222222222222222222 2222222222222222222222222222 22222222222222222222222222222 222222222222222222222222222222 |
10648 10941048 10970645048 10973607685048 10973903978085048 10973933607682085048 10973936570644722085048 10973936866941015122085048 10973936896570644719122085048 10973936899533607681759122085048 10973936899829903978052159122085048 10973936899859533607681756159122085048 10973936899862496570644718796159122085048 10973936899862792866941015089196159122085048 10973936899862822496570644718793196159122085048 10973936899862825459533607681755833196159122085048 10973936899862825755829903978052126233196159122085048 10973936899862825785459533607681755830233196159122085048 10973936899862825788422496570644718792870233196159122085048 10973936899862825788718792866941015089163270233196159122085048 10973936899862825788748422496570644718792867270233196159122085048 10973936899862825788751385459533607681755829907270233196159122085048 10973936899862825788751681755829903978052126200307270233196159122085048 10973936899862825788751711385459533607681755829904307270233196159122085048 10973936899862825788751714348422496570644718792866944307270233196159122085048 10973936899862825788751714644718792866941015089163237344307270233196159122085048 10973936899862825788751714674348422496570644718792866941344307270233196159122085048 10973936899862825788751714677311385459533607681755829903981344307270233196159122085048 10973936899862825788751714677607681755829903978052126200274381344307270233196159122085048 |
| n | Zahl | 3. Potenz |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
33 333 3333 33333 333333 3333333 33333333 333333333 3333333333 33333333333 333333333333 3333333333333 33333333333333 333333333333333 3333333333333333 33333333333333333 333333333333333333 3333333333333333333 33333333333333333333 333333333333333333333 3333333333333333333333 33333333333333333333333 333333333333333333333333 3333333333333333333333333 33333333333333333333333333 333333333333333333333333333 3333333333333333333333333333 33333333333333333333333333333 333333333333333333333333333333 |
35937 36926037 37025927037 37035925937037 37036925926037037 37037025925927037037 37037035925925937037037 37037036925925926037037037 37037037025925925927037037037 37037037035925925925937037037037 37037037036925925925926037037037037 37037037037025925925925927037037037037 37037037037035925925925925937037037037037 37037037037036925925925925926037037037037037 37037037037037025925925925925927037037037037037 37037037037037035925925925925925937037037037037037 37037037037037036925925925925925926037037037037037037 37037037037037037025925925925925925927037037037037037037 37037037037037037035925925925925925925937037037037037037037 37037037037037037036925925925925925925926037037037037037037037 37037037037037037037025925925925925925925927037037037037037037037 37037037037037037037035925925925925925925925937037037037037037037037 37037037037037037037036925925925925925925925926037037037037037037037037 37037037037037037037037025925925925925925925925927037037037037037037037037 37037037037037037037037035925925925925925925925925937037037037037037037037037 37037037037037037037037036925925925925925925925925926037037037037037037037037037 37037037037037037037037037025925925925925925925925925927037037037037037037037037037 37037037037037037037037037035925925925925925925925925925937037037037037037037037037037 37037037037037037037037037036925925925925925925925925925926037037037037037037037037037037 |
| n | Zahl | 3. Potenz |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
66 666 6666 66666 666666 6666666 66666666 666666666 6666666666 66666666666 666666666666 6666666666666 66666666666666 666666666666666 6666666666666666 66666666666666666 666666666666666666 6666666666666666666 66666666666666666666 666666666666666666666 6666666666666666666666 66666666666666666666666 666666666666666666666666 6666666666666666666666666 66666666666666666666666666 666666666666666666666666666 6666666666666666666666666666 66666666666666666666666666666 666666666666666666666666666666 |
287496 295408296 296207416296 296287407496296 296295407408296296 296296207407416296296 296296287407407496296296 296296295407407408296296296 296296296207407407416296296296 296296296287407407407496296296296 296296296295407407407408296296296296 296296296296207407407407416296296296296 296296296296287407407407407496296296296296 296296296296295407407407407408296296296296296 296296296296296207407407407407416296296296296296 296296296296296287407407407407407496296296296296296 296296296296296295407407407407407408296296296296296296 296296296296296296207407407407407407416296296296296296296 296296296296296296287407407407407407407496296296296296296296 296296296296296296295407407407407407407408296296296296296296296 296296296296296296296207407407407407407407416296296296296296296296 296296296296296296296287407407407407407407407496296296296296296296296 296296296296296296296295407407407407407407407408296296296296296296296296 296296296296296296296296207407407407407407407407416296296296296296296296296 296296296296296296296296287407407407407407407407407496296296296296296296296296 296296296296296296296296295407407407407407407407407408296296296296296296296296296 296296296296296296296296296207407407407407407407407407416296296296296296296296296296 296296296296296296296296296287407407407407407407407407407496296296296296296296296296296 296296296296296296296296296295407407407407407407407407407408296296296296296296296296296296 |
Periodische Strukturen gibt es bei der 3. Potenz nur bei Schnapszahlen der Ziffer 3 und 6. Folgende Sequenzen treten auf. Die Sequenzen lassen mehrere Interpretationen zu (Rotation bzw. Permutation der Ziffernfolge).
| Basis | Sequenz | Primfaktorzerlegung | |
| 3 | 259 592 925 370 703 037 |
7·37 2·2·2·2·37 5·5·37 2·5·37 19·37 1·37 |
7·37 16·37 25·37 10·37 19·37 1·37 |
| 6 | 296 962 629 407 074 740 |
2·2·2·37 2·13·37 17·37 11·37 2·37 2·2·5·37 |
8·37 26·37 17·37 11·37 2·37 20·37 |
Alle Sequenzen enthalten den Faktor 37.
Wenn dreistellige Zahlen abc durch 37 teilbar sind dann sind auch alle Permutationen (bca und cab) durch 37 teilbar. Ausserdem sind alle dreistelligen Schnapszahlen durch 37 teilbar.
| 1·37 = 37 2·37 = 74 3·37 = 111 4·37 = 148 5·37 = 185 6·37 = 222 7·37 = 259 8·37 = 296 9·37 = 333 |
10·37 = 370 11·37 = 407 12·37 = 444 13·37 = 481 14·37 = 518 15·37 = 555 16·37 = 592 17·37 = 629 18·37 = 666 |
19·37 = 703 20·37 = 740 21·37 = 777 22·37 = 814 23·37 = 851 24·37 = 888 25·37 = 925 26·37 = 962 27·37 = 999 |
Bei der 4. Potenz gibt es periodische Sequenzen nur bei Schnapszahlen der Ziffer 3 und 6.
| n | Zahl | 4. Potenz |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
33 333 3333 33333 333333 3333333 33333333 333333333 3333333333 33333333333 333333333333 3333333333333 33333333333333 333333333333333 3333333333333333 33333333333333333 333333333333333333 3333333333333333333 33333333333333333333 333333333333333333333 3333333333333333333333 33333333333333333333333 333333333333333333333333 3333333333333333333333333 33333333333333333333333333 333333333333333333333333333 3333333333333333333333333333 33333333333333333333333333333 333333333333333333333333333333 |
1185921 12296370321 123407414814321 1234518519259254321 12345629629703703654321 123456740740748148147654321 1234567851851852592592587654321 12345678962962963037037036987654321 123456790074074074081481481480987654321 1234567901185185185185925925925920987654321 12345679012296296296296370370370370320987654321 123456790123407407407407414814814814814320987654321 1234567901234518518518518519259259259259254320987654321 12345679012345629629629629629703703703703703654320987654321 123456790123456740740740740740748148148148148147654320987654321 1234567901234567851851851851851852592592592592592587654320987654321 12345679012345678962962962962962963037037037037037036987654320987654321 123456790123456790074074074074074074081481481481481481480987654320987654321 1234567901234567901185185185185185185185925925925925925925920987654320987654321 12345679012345679012296296296296296296296370370370370370370370320987654320987654321 123456790123456790123407407407407407407407414814814814814814814814320987654320987654321 1234567901234567901234518518518518518518518519259259259259259259259254320987654320987654321 12345679012345679012345629629629629629629629629703703703703703703703703654320987654320987654321 123456790123456790123456740740740740740740740740748148148148148148148148147654320987654320987654321 1234567901234567901234567851851851851851851851851852592592592592592592592592587654320987654320987654321 12345679012345679012345678962962962962962962962962963037037037037037037037037036987654320987654320987654321 123456790123456790123456790074074074074074074074074074081481481481481481481481481480987654320987654320987654321 1234567901234567901234567901185185185185185185185185185185925925925925925925925925925920987654320987654320987654321 12345679012345679012345679012296296296296296296296296296296370370370370370370370370370370320987654320987654320987654321 |
| n | Zahl | 4. Potenz |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
66 666 6666 66666 666666 6666666 66666666 666666666 6666666666 66666666666 666666666666 6666666666666 66666666666666 666666666666666 6666666666666666 66666666666666666 666666666666666666 6666666666666666666 66666666666666666666 666666666666666666666 6666666666666666666666 66666666666666666666666 666666666666666666666666 6666666666666666666666666 66666666666666666666666666 666666666666666666666666666 6666666666666666666666666666 66666666666666666666666666666 666666666666666666666666666666 |
18974736 196741925136 1974518637029136 19752296308148069136 197530074075259258469136 1975307851851970370362469136 19753085629629641481481402469136 197530863407407408592592591802469136 1975308641185185185303703703695802469136 19753086418962962962974814814814735802469136 197530864196740740740741925925925925135802469136 1975308641974518518518518637037037037029135802469136 19753086419752296296296296308148148148148069135802469136 197530864197530074074074074075259259259259258469135802469136 1975308641975307851851851851851970370370370370362469135802469136 19753086419753085629629629629629641481481481481481402469135802469136 197530864197530863407407407407407408592592592592592591802469135802469136 1975308641975308641185185185185185185303703703703703703695802469135802469136 19753086419753086418962962962962962962974814814814814814814735802469135802469136 197530864197530864196740740740740740740741925925925925925925925135802469135802469136 1975308641975308641974518518518518518518518637037037037037037037029135802469135802469136 19753086419753086419752296296296296296296296308148148148148148148148069135802469135802469136 197530864197530864197530074074074074074074074075259259259259259259259258469135802469135802469136 1975308641975308641975307851851851851851851851851970370370370370370370370362469135802469135802469136 19753086419753086419753085629629629629629629629629641481481481481481481481481402469135802469135802469136 197530864197530864197530863407407407407407407407407408592592592592592592592592591802469135802469135802469136 1975308641975308641975308641185185185185185185185185185303703703703703703703703703695802469135802469135802469136 19753086419753086419753086418962962962962962962962962962974814814814814814814814814814735802469135802469135802469136 197530864197530864197530864196740740740740740740740740740741925925925925925925925925925925135802469135802469135802469136 |
33333333333333333333333334 = 123456790 123456790 123456740 740 740 740 740 740 740 740 748 148 148 148 148 148 148 148 14765432 098765432 098765432 1
333333333333333333333333334 = 123456790 123456790 123456785 185 185 185 185 185 185 185 185 259 259 259 259 259 259 259 259 258765432 098765432 098765432 1
3333333333333333333333333334 = 123456790 123456790 123456789 629 629 629 629 629 629 629 629 630 370 370 370 370 370 370 370 370 3698765432 098765432 098765432 1
66666666666666666666666664 = 197530864 197530864 197530785 185 185 185 185 185 185 185 1970 370 370 370 370 370 370 370 3624691 358024691 358024691 36
666666666666666666666666664 = 197530864 197530864 197530856 296 296 296 296 296 296 296 296 41 481 481 481 481 481 481 481 481 4024691 358024691 358024691 36
6666666666666666666666666664 = 197530864 197530864 197530863 407 407 407 407 407 407 407 407 408 592 592 592 592 592 592 592 592 591 8024691 358024691 358024691 36
Alle Zahlen zeigen am Anfang und am Ende 9 stellige Sequenzen und in der Mitte zwei 3 stellige Sequenzen. Bei den 3 stelligen Sequenzen gibt es mehrere Interpretationsmöglichkeiten (Rotation bzw. Permutation der Ziffernfolge) aber alle sind durch 37 teilbar.
| Basis | Sequenz | Primfaktorzerlegung | |
| 3 | 123456790 740 148 185 259 629 370 098765432 |
2·5·37·333667 2·2·5·37 2·2·37 5·37 7·37 17·37 2·5·37 2·2·2·37·333667 |
10·37·333667 20·37 4·37 5·37 7·37 17·37 10·37 8·37·333667 |
| 6 | 197530864 185 370 296 481 407 592 358024691 |
2·2·2·2·37·333667 5·37 2·5·37 2·2·2·37 13·37 11·37 2·2·2·2·37 29·37·333667 |
16·37·333667 5·37 10·37 8·37 13·37 11·37 16·37 29·37·333667 |
Alle Sequenzen in der Form abcabcabc sind durch 333667 teilbar, ein paar Beispiele.
| Sequenz | Primfaktorzerlegung | |
| 148148148 185185185 259259259 296296296 370370370 407407407 481481481 592592592 629629629 740740740 |
2·2·3·37·333667 3·5·37·333667 3·7·37·333667 2·2·2·3·37·333667 2·3·5·37·333667 3·11·37·333667 3·13·37·333667 2·2·2·2·3·37·333667 3·17·37·333667 2·2·3·5·37·333667 |
12·37·333667 15·37·333667 21·37·333667 24·37·333667 30·37·333667 33·37·333667 39·37·333667 48·37·333667 51·37·333667 60·37·333667 |
In höheren Potenzen von Schnapszahlen konnte ich keine periodischen Strukturen entdecken.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |