[zurück]

12. Vollkommenen Zahlen, Befreundete Zahlen, Narzisstische Zahlen

 [vor]

Eine natürliche Zahl n ist dann eine vollkommene Zahl, wenn sie gleich der Summe aller ihrer (positiven) Teiler außer sich selbst ist. Es gilt:

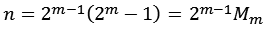
Wenn Mm eine Mersenne Primzahl ist dann ist n eine vollkommene Zahl. Ein paar Beispiele.

m = 2
n = 21 M2 = 2 * 3 = 6 = 1 + 2 + 3

m = 3
n = 22 M3 = 4 * 7 = 28 = 1 + 2 + 4 + 7 + 14

m = 5
n = 24 M5 = 16 * 31 = 496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248

m = 7
n = 26 M7 = 64 * 127 = 8128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064

m = 13
n = 212 M13 = 4096 * 8191 = 33550336

m = 17
n = 216 M17 = 65536 * 131071 = 8589869056

m = 19
n = 218 M19 = 262144 * 524287 = 137438691328

m = 31
n = 230 M31 = 1073741824 * 2147483647 = 2305843008139952128

m = 61
n = 260 M61 = 1152921504606846976 * 2305843009213693951 = 2658455991569831744654692615953842176

Die perfekten Zahlen enden immer auf 6 oder 8 (bzw. 28).

Die Summe der Kehrwerte aller Teiler der vollkommenen Zahlen ergibt immer 2, ein paar Beispiele

n
6      
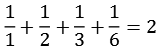28      
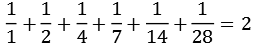496      
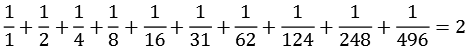8128      

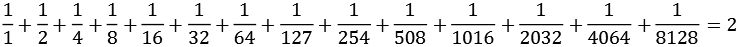Jede gerade vollkommene Zahl n lässt sich darstellen als Summe der ersten natürlichen Zahlen.

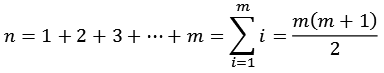
mit

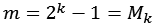
m
3      
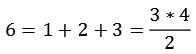78      
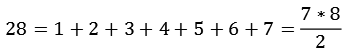31      
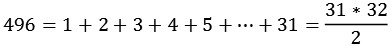127      

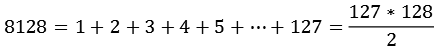Mit Ausnahme von 6 lässt sich jede gerade vollkommene Zahl n aus der Summe der Kuben der ersten ungeraden natürlichen Zahlen darstellen.

28 = 13 + 33 = 1 + 27

496 = 13 + 33 + 53 + 73 = 1 + 27 + 125 + 343

8128 = 13 + 33 + 53 + 73 + 93 + 113 + 133 + 153 = 1 + 27 + 125 + 343 + 729 + 1331 + 2197 + 3375

Jede gerade vollkommene Zahl lässt sich mit einer geeigneten natürlichen Zahl k darstellen.

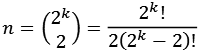
k = 2
n = 6

k = 3
n = 28

k = 5
n = 496

k = 7
n = 8128

Auch die Darstellung im Dualsystem ist interessant. Eine gerade vollkommene Zahl erscheint im Dualsystem als charakteristische Folge von Einsen und Nullen , und zwar aus a+1 Einsen und a Nullen.

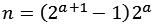
a = 1
n = 6 = 110

a = 2
n = 28 = 11100

a = 4
n = 496 = 111110000

a = 6
n = 8128 = 1111111000000

a = 12
n = 33550336 = 1111111111111000000000000

a = 16
n = 8589869056 = 111111111111111110000000000000000

a = 18
n = 137438691328 = 1111111111111111111000000000000000000

a = 30
n = 2305843008139952128 = 1111111111111111111111111111111000000000000000000000000000000

a = 60
n = 2658455991569831744654692615953842176 = 1111111111111111111111111111111111111111111111111111111111111000000000000000000000000000000000000000000000000000000000000

Befreundete Zahlen

Zwei verschiedene natürliche Zahlen, von denen wechselseitig jeweils eine Zahl gleich der Summe der echten Teiler der anderen Zahl ist, werden befreundete Zahlen genannt. Ein paar Beispiele:

220 : 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
284 : 1 + 2 + 4 + 71 + 142 = 220

1184 : 1+2+4+8+16+32+37+74+148+296+592 = 1210
1210 : 1+2+5+10+11+22+55+110+121+242+605 = 1184

2620 : 1+2+4+5+10+20+131+262+524+655+1310 = 2924
2924 : 1+2+4+17+34+43+68+86+172+731+1462 = 2620

5020 : 1+2+4+5+10+20+251+502+1004+1255+2510 = 5564
5564 : 1+2+4+13+26+52+107+214+428+1391+2782 = 5020

6232 : 1+2+4+8+19+38+41+76+82+152+164+328+779+1558+3116 = 6368
6368 : 1+2+4+8+16+32+199+398+796+1592+3184 = 6232

10744 : 1+2+4+8+17+34+68+79+136+158+316+632+1343+2686+5372 = 10856
10856 : 1+2+4+8+23+46+59+92+118+184+236+472+1357+2714+5428 = 10744

12285 : 1+3+5+7+9+13+15+21+27+35+39+45+63+65+91+105+117+135+189+195+273+315+351+455+585+819+945+1365+1755+2457+4095 = 14595
14595 : 1+3+5+7+15+21+35+105+139+417+695+973+2085+2919+4865 = 12285

17296 : 1+2+4+8+16+23+46+47+92+94+184+188+368+376+752+1081+2162+4324+8648 = 18416
18416 : 1+2+4+8+16+1151+2302+4604+9208 = 17296

9363584 : 1+2+4+8+16+32+64+128+191+382+383+764+766+1528+1532+3056+3064+6112+6128+12224+12256+24448+24512+49024+73153+146306+292612+585224+1170448+2340896+4681792 = 9437056
9437056 : 1+2+4+8+16+32+64+128+73727+147454+294908+589816+1179632+2359264+4718528 = 9363584

Satz von Thabit Ibn Qurra

Für eine natürliche Zahl n sei

Wenn x, y und z ungerade Primzahlen (blau) sind, dann sind die beiden Zahlen

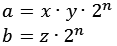
befreundet.

n x y z a b
1    5    2    17    20    34   
2    11    5    71    220    284   
3    23    11    287    2024    2296   
4    47    23    1151    17296    18416   
5    95    47    4607    142880    147424   
6    191    95    18431    1161280    1179584   
7    383    191    73727    9363584    9437056   
8    767    383    294911    75202816    75497216   
9    1535    767    1179647    602800640    603979264   
10    3071    1535    4718591    4827120640    4831837184   

Narzisstische Zahlen

Diese n-stelligen Zahlen entsprechen der Summe der n-ten Potenz ihrer Ziffern. 153 ist kleinste Zahl dieser Gruppe, die bisher größte entdeckte narzisstische Zahl lautet 115132219018763992565095597973971522401, die 39 Stellen hat, d.h. die Summe jeder einzelnen Ziffer in die 39. Potenz erhoben ergibt die Zahl selbst.

153 = 13 + 53 + 33 = 1 + 125 + 27
370 = 33 + 73 + 03 = 27 + 343 + 0
371 = 33 + 73 + 13 = 27 + 343 + 1
407 = 43 + 03 + 73 = 64 + 0 + 343

1634 = 14 + 64 + 34 + 44 = 1 + 1296 + 81 + 256
8208 = 84 + 24 + 04 + 84 = 4096 + 16 + 0 + 4096
9474 = 94 + 44 + 74 + 44 = 6561 + 256 + 2401 + 256

54748 = 55 + 45 + 75 + 45 + 85 = 3125 + 1024 + 16807 + 1024 + 32768
92727 = 95 + 25 + 75 + 25 + 75 = 59049 + 32 + 16807 + 32 + 16807
93084 = 95 + 35 + 05 + 85 + 45 = 59049 + 243 + 0 + 32768 + 1024

548834 = 56 + 46 + 86 + 86 + 36 + 46 = 15625 + 4096 + 262144 + 262144 + 729 + 4096

Insgesamt sind 88 narzisstische Zahlen bekannt. Endet eine narzisstische Zahl n auf Null, dann ist auch die folgende Zahl (n + 1) eine narzisstische Zahl, da 0n = 0 und 1n = 1.
Zum Beispiel

0, 1
370, 371
24678050, 24678051
32164049650, 32164049651
4338281769391370, 4338281769391371
3706907995955475988644380, 3706907995955475988644381
19008174136254279995012734740, 19008174136254279995012734741
186709961001538790100634132976990, 186709961001538790100634132976991
115132219018763992565095597973971522400, 115132219018763992565095597973971522401

Alle 88 narzisstischen Zahlen.

n
1    0   
1   
2   
3   
4   
5   
6   
7   
8   
9   
3    153   
370   
371   
407   
4    1634   
8208   
9474   
5    54748   
92727   
93084   
6    548834   
7    1741725   
4210818   
9800817   
9926315   
8    24678050   
24678051   
88593477   
9    146511208   
472335975   
534494836   
912985153   
10    4679307774   
11    32164049650   
32164049651   
40028394225   
42678290603   
44708635679   
49388550606   
82693916578   
94204591914   
14    28116440335967   
16    4338281769391370   
4338281769391371   
17    21897142587612075   
35641594208964132   
35875699062250035   
19    1517841543307505039   
3289582984443187032   
4498128791164624869   
4929273885928088826   
20    63105425988599693916   
21    128468643043731391252   
449177399146038697307   
23    21887696841122916288858   
27879694893054074471405   
27907865009977052567814   
28361281321319229463398   
35452590104031691935943   
24    174088005938065293023722   
188451485447897896036875   
239313664430041569350093   
25    1550475334214501539088894   
1553242162893771850669378   
3706907995955475988644380   
3706907995955475988644381   
4422095118095899619457938   
27    121204998563613372405438066   
121270696006801314328439376   
128851796696487777842012787   
174650464499531377631639254   
177265453171792792366489765   
29    14607640612971980372614873089   
19008174136254279995012734740   
19008174136254279995012734741   
23866716435523975980390369295   
31    1145037275765491025924292050346   
1927890457142960697580636236639   
2309092682616190307509695338915   
32    17333509997782249308725103962772   
33    186709961001538790100634132976990   
186709961001538790100634132976991   
34    1122763285329372541592822900204593   
35    12639369517103790328947807201478392   
12679937780272278566303885594196922   
37    1219167219625434121569735803609966019   
38    12815792078366059955099770545296129367   
39    115132219018763992565095597973971522400   
115132219018763992565095597973971522401   

Narzisstische Zahlen mit steigender Potenz

Narzisstische Zahlen mit steigender Potenz sind Zahlen, deren Summe ihrer Ziffern, potenziert mit deren Stelle in der Zahl, die Zahl selbst ergibt. Also zum Beispiel eine Zahl abc = a1 + b2 + c3.
Ein paar Beispiele:

89 = 81 + 92 = 8 + 81

135 = 11 + 32 + 53 = 1 + 9 + 125

175 = 11 + 72 + 53 = 1 + 49 + 125

518 = 51 + 12 + 83 = 5 + 1 + 512

598 = 51 + 92 + 83 = 5 + 81 + 512

1306 = 11 + 32 + 03 + 64 = 1 + 9 + 0 + 1296

1676 = 11 + 62 + 73 + 64 = 1 + 36 + 343 + 1296

2427 = 21 + 42 + 23 + 74 = 2 + 16 + 8 + 2401

2646798 = 21 + 62 + 43 + 64 + 75 + 96 + 87 = 2 + 36 + 64 + 1296 + 16807 + 531441 + 2097152

12157692622039623539 = 11 + 22 + 13 + 54 + 75 + 66 + 97 + 28 + 69 + 210 + 211 + 012 + 313 + 914 + 615 + 216 + 317 + 518 + 319 + 920 =

[zurück] [Inhaltsverzeichnis] [vor]